|
|||||
|
|
| 频率域电磁法三维有限元正演线性方程组迭代算法 | |
| 引用本文: | 秦策, 王绪本, 赵宁, 曹礼刚. 2020. 频率域电磁法三维有限元正演线性方程组迭代算法. 地球物理学报, 63(8): 3180-3191, doi: 10.6038/cjg2020N0194 |
| 作者姓名: | 秦策 王绪本 赵宁 曹礼刚 |
| 作者单位: | 1. 河南理工大学物理与电子信息学院, 河南焦作 454000; 2. 成都理工大学地球物理学院, 成都 610059 |
| 基金项目: | 国家自然科学基金项目(41904078,U1704128,41674078),国家重点研发计划项目(2018YFC0603602,2017YFC0601806,2018YFC0603300)和河南理工大学博士基金项目(B2019-17)联合资助. |
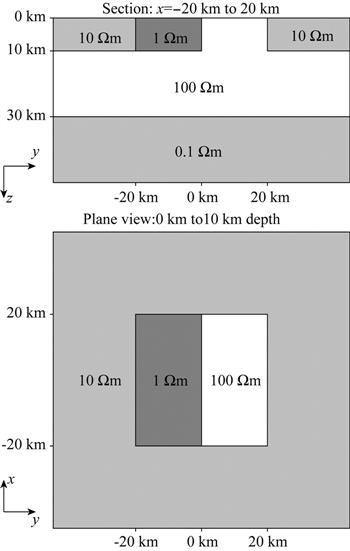
| 摘 要: |  在三维频率域电磁法的正演模拟方法中,有限元方法具有计算精度高、适应性强的优点,近年来来得到了越来越多的关注.在正演过程中,主要的计算量集中在求解由偏微分方程组离散得到的线性方程组上,因此求解线性方程组关系着正演计算速度以及模拟精度.由于由有限元方法离散得到的复系数线性方程组条件数非常大,使用常规的迭代法和预条件很难收敛.目前大多数的研究工作采用直接解法,需要大量的计算机内存,限制了可求解问题的规模. 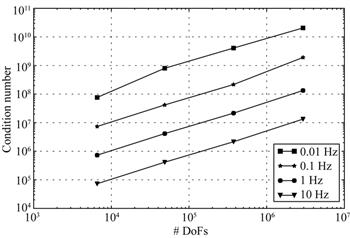 |
| 关 键 词: | 线性方程组 迭代算法 辅助空间预条件 频率域电磁法 矢量有限元 |
| 收稿时间: | 2019-05-15 |
| 修稿时间: | 2020-06-05 |
| 本文献已被 CNKI 等数据库收录! | |
| 点击此处可从《地球物理学报》浏览原始摘要信息 | |
| 点击此处可从《地球物理学报》下载免费的PDF全文 | |