
|
|||||
|
|
| 综合三维激光与建筑信息模型的精密测量应用 | |
| 引用本文: | 赵志胜, 陈宇, 王彬. 利用非线性高斯-赫尔默特模型与抗差估计的点云拟合方法[J]. 武汉大学学报 ( 信息科学版), 2024, 49(7): 1201-1211. DOI: 10.13203/j.whugis20220072 |
| 作者姓名: | 赵志胜 陈宇 王彬 |
| 作者单位: | 1.南京工业大学测绘科学与技术学院,江苏南京,211816 |
| 基金项目: | 国家自然科学基金(42004002)。 |
| 摘 要: | 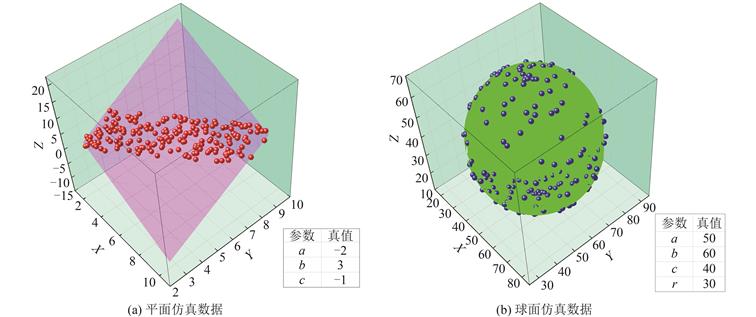 目前已有的点云拟合方法大多是在线性的高斯-马尔可夫(Gauss-Markov,GM)或变量误差(errors-in-variables,EIV)模型基础上提出的,无法严格适用于非线性的曲面拟合问题。将点云拟合的数学模型统一抽象为更具一般性的非线性高斯-赫尔默特(Gauss-Helmert,GH)模型,并针对数据存在粗差的情况,引入等价权抗差方案,提出了一种基于抗差非线性GH(robust nonlinear GH,RGH)模型的点云拟合方法。 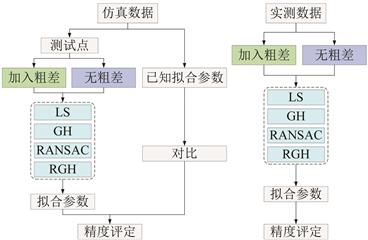 |
| 关 键 词: | 点云拟合 粗差 非线性GH模型 抗差估计 标准化残差 |
| 收稿时间: | 2022-11-25 |
| 点击此处可从《武汉大学学报(信息科学版)》浏览原始摘要信息 | |
| 点击此处可从《武汉大学学报(信息科学版)》下载免费的PDF全文 | |
