基于集合平滑数据同化与直接采样法融合水文地球物理数据刻画裂隙网络分布

焦婷婷; 邓亚平; 钱家忠; 骆乾坤

doi:10.16030/j.cnki.issn.1000-3665.202310004

基于集合平滑数据同化与直接采样法融合水文地球物理数据刻画裂隙网络分布

合肥工业大学资源与环境工程学院，安徽合肥　230009

基金项目: 国家自然科学青年基金项目（42102283）；中央高校基本科研费专项项目（JZ2023HGTB0235）

详细信息

作者简介: 焦婷婷（1996—），女，硕士研究生，主要从事地下水数值模拟研究。E-mail：2021110687@mail.hfut.edu.cn

通讯作者: 邓亚平（1989—），女，博士，讲师，主要从事水文地球物理和水文地质参数反演等领域的研究。E-mail：dengyaping@hfut.edu.cn

中图分类号: P641.2

收稿日期: 2023-10-02

修回日期: 2023-12-18

刊出日期: 2024-07-15

Characterizing fracture networks by integrating hydrogeophysical data based on the ESMDA-DS method

School of Resources and Environmental Engineering, Hefei University of Technology, Hefei, Anhui　230009, China

More Information

Corresponding author: DENG Yaping, dengyaping@hfut.edu.cn

Received Date: 02 October 2023

Revised Date: 18 December 2023

Publish Date: 15 July 2024

摘要

摘要:
刻画裂隙含水层在地下水污染、地热、油气资源开采等研究中起关键作用。由于裂隙介质的强非均质性，其渗透率场一般呈现出显著的非高斯特性，该特性给水文地质参数的推估带来了极大的困难与挑战。为解决裂隙介质参数推估难的问题，本研究利用集合平滑数据同化与直接采样法融合水文地球物理数据推估裂隙介质参数场，设计多个数值算例，探究该数据同化框架刻画裂隙介质参数场的有效性，分析同化3种不同类型的观测数据对参数推估结果的影响，并探讨裂隙密度以及观测井的数量对参数推估效果的影响。研究结果表明：（1）基于集合平滑数据同化与直接采样法融合水文地球物理数据的方法，可有效地推估裂隙介质水文地质参数空间分布；（2）对比3种类型的观测数据推估结果，可知同时融合水头和自然电位观测数据（水文地球物理数据）的参数推估效果最佳；（3）研究区的裂隙密度以及观测井的数量同样对数据同化结果产生影响，因此建议在实际应用中应选择合理的观测井数量从而获得最优的参数推估方案。该研究可为裂隙介质参数场的刻画提供一种有效的方法，进一步为裂隙水资源的开发和管理提供可靠的理论依据。
- 裂隙 /
- 水文地球物理方法 /
- 数据同化 /
- 多点地质统计 /
- 参数推估
Abstract:
Characterizing fractured aquifers plays a crucial role in the issues related to groundwater contamination, and geothermal and hydrocarbon resource exploitation. Due to the heterogeneity of the fractured medium, the permeability of fractured medium generally exhibits significant non-Gaussian characteristics, leading to difficulties and challenges in the estimation of hydrogeological parameters. This study used the ESMDA-DS (ensemble smoother with multiple data assimilation-direct sampling) integrating hydrogeophysical data to explore the effectiveness of the data assimilation framework in portraying the parameter field of the fractured medium and to analyze the influences of assimilating three different types of observation data, the fracture density, and the number of observation wells on the parameter estimation. The results show that the method of ESMDA-DS integrating hydrogeophysical data can estimate the spatial distribution of hydrogeological parameters in the fractured medium effectively. Comparing the estimated results from three types of observation, it finds that fusing the hydraulic head and the self-potential observational data (hydrogeophysical data) has the best effect. The fracture density in the study area and the number of observation wells also affect the data assimilation results. A reasonable number of observation wells is suggested to obtain the optimal parameter estimation scheme in practical applications. This study can provide an effective method for characterizing the parameter field of the fractured medium and a reliable theoretical basis for the development and management of fractured water resources.
- fracture /
- hydrogeophysical method /
- data assimilation /
- multi-point geostatistics /
- parametric inversion

HTML全文

裂隙是地下水的主要贮存空间之一。裂隙水文地质参数的准确识别对裂隙水资源的有效管理、污染物迁移分布的准确预测、地热及非常规油气等资源的开发都具有重大意义^{[1 − 6]}。然而，由于裂隙介质具有强非均质性和不连续性，其水文地质参数也存在巨大的空间变异性，因此如何精确识别裂隙介质的水文地质参数变得极具挑战性。

传统的参数推估方法有直接野外测量、试验井法等，这些方法通常计算效率不高且推估精度不佳。因此，引入了数据同化方法。目前常见的数据同化方法包括，卡尔曼滤波算法（Kalman filter，KF）^[7]、集合平滑方法（ensemble smoother，ES）^{[8 − 9]}、集合卡尔曼滤波算法（ensemble Kalman filter，EnKF）^{[10 − 12]}、迭代的集合平滑方法（iterative ensemble smoother，IES）^{[13 − 14]}。比起其他方法， Emerick等^[15]提出的集合平滑数据同化方法（ensemble smoother with multiple data assimilation，ESMDA）在数据拟合和参数推估效果方面表现更为突出，且计算成本更低^{[16 − 17]}。

现有的数据同化方法一般仅可处理服从高斯分布的参数场^{[18 − 20]}。由于裂隙介质的强非均质性，其水文地质参数一般呈非高斯分布。目前，广泛使用多点地质统计学方法解决非高斯场问题。多点地质统计学方法众多，包括Strebelle等^{[21 − 22]}提出的顺序正态方程模拟方法（sequential normal equations simulation，SNESIM），Arpat等^[23]提出的模式模拟方法（simulation of patterns，SIMPAT），Zhang等^[24]提出的基于滤波器的模拟方法（filter-based simulation，FILTERSIM），Mariethoz等^[25]提出直接采样法（direct sampling，DS）。相比于其他方法而言，DS方法结合逐点模拟和模式模拟方法的优势，利用顺序模拟的策略，计算时间短且计算效率高。DS方法虽能保持参数场的非高斯特性，但无法融合多源观测数据确保推估精度。

为解决DS方法融合动态数据的难题，有学者将DS方法与数据同化方法进行耦合。Cao等^[26]构建了迭代的集合平滑方法与直接采样法（iterative ensemble smoother-direct sampling，IES-DS）数据同化框架；宗成元等^[27]提出了一种新的数据同化方法——集合平滑数据同化与直接采样法（ensemble smoother with multiple data assimilation-direct sampling，ESMDA-DS），但其只融合了水头、浓度等“硬数据”，并没有融合其他类型的观测数据。值得注意是，前人研究中提出的数据同化框架大多应用于多孔介质，对裂隙介质的研究较少；其次，大多数研究仅通过同化水头和浓度数据等推估参数场，较少关注同化多种类型的观测数据。然而，水头、浓度等“硬数据”的获取方法主要是基于钻孔采样，该方法获取成本较高，导致其最终获取的直接观测数据量较少。相比之下，自然电位、电阻率等地球物理数据获取成本较低，且易获取丰富的数据^{[28 − 32]}。因此融合地球物理数据对裂隙介质进行参数推估具有重要意义。

针对上述问题，本文提出基于ESMDA-DS融合水头（hydraulic-head，H）和自然电位（self-potential，SP）数据的方法刻画裂隙网络水文地质参数。该方法结合了DS与ESMDA方法各自的优势，在保持裂隙参数场非高斯特性的基础上，同时融合水文地质数据（如水头）和地球物理数据（如自然电位），以提高裂隙介质对数渗透率场的推估精度。本文通过构建多组数值算例，系统探讨了融合不同类型观测数据对推估结果精度和不确定性的影响。同时，还分析了裂隙密度和观测井数量对参数推估结果的影响。

1. 研究方法

1.1 直接采样法

多点地质统计学方法在地质领域中应用广泛^{[33 − 35]}，通常用于模拟非高斯场。其中，DS方法是一种高效且明显优越的算法。该方法基于训练图像，替代了概念地质模型，直接提取表征多点之间空间信息的特征，在非均质介质建模和解决复杂地质问题方面具有显著优势。

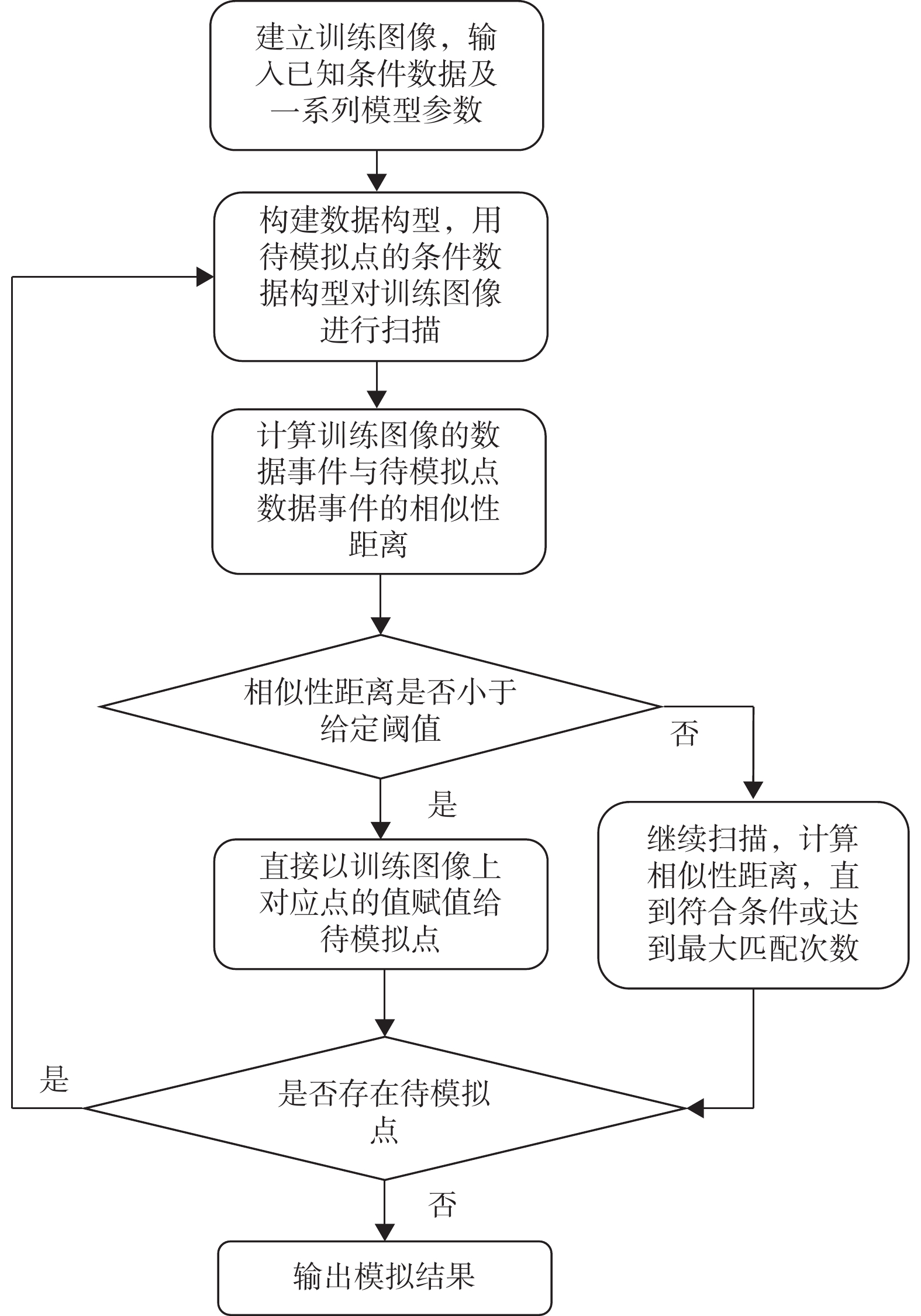
DS方法主要步骤如图1所示。

图 1. DS方法主要步骤流程图

Figure 1. Flowchart of the main steps of the DS algorithm

下载: 全尺寸图片幻灯片

步骤1：建立训练图像，输入已知条件点作为模拟的已知条件数据，并定义模拟过程的一系列模型参数，如数据事件的最大条件点数、训练图像搜索比例、相似性距离的阈值等。

步骤2：构建数据构型，对于任意待模拟网格点，分析其相对应的条件数据的数据构型，如没有条件数据，则进行其他待模拟网格点的搜索。

步骤3：从周围条件点数据最多的待模拟网格点开始模拟，使用待模拟网格点的条件数据构型对训练图像进行搜索。

步骤4：计算训练图像中的数据事件与待模拟网格中的数据事件间的距离。若距离小于设定的相似性距离的阈值，则将训练图像上的此点赋值给待模拟网格点。

步骤5：若超过设定的相似性距离的阈值，则会持续随机扫描训练图像，直到找到符合条件的点为止。若一直无法找到符合条件的点且达到最大匹配次数，则选择距离最近的数据事件作为最终结果。

步骤6：将模拟所得的值作为已知条件点加入到下一点的模拟中，同时应优先将步骤1中输入的已知条件点作为备选。

步骤7：重复以上步骤，直到所有点都被模拟为止。

1.2 集合平滑数据同化方法

ESMDA方法^[15]是一种常用的数据同化方法，其基本原理与集合平滑方法类似。然而，ESMDA方法在迭代过程中引入了多次迭代，以便更好地拟合观测数据，这是其与集合平滑方法的不同之处。此外，ESMDA方法在处理观测误差协方差矩阵时，引入了膨胀系数，有效地解决了可能出现的过拟合问题。

步骤1：确定初始集合大小（N_e），迭代次数（N_a），膨胀系数（ ${{\alpha }_i}$ ）（i=1, 2, ···, N_a）。

$\sum\limits_{i = 1}^{N_{{\mathrm{a}}}} {\frac{1}{{{{\alpha }_i}}}} = 1,\;i = 1,2,\cdots,N_{{\mathrm{a}}}$

(1)

式中： ${{\alpha }_i}$ ——第i次的膨胀系数。

本研究中， ${{\alpha }_i}$ 的取值为：α₁=9.333，α₂=7.000，α₃=4.000，α₄=3.000^[11]。

步骤2：针对每个样本的初始估计，基于上次迭代中更新得到的模型参数，运行正演模型以获取该样本对应的模拟数据。

$\boldsymbol{d}_i^l=\boldsymbol{G}(\boldsymbol{X}_i^l),\; i=1,2,\cdots,N_{{\mathrm{e}}}$

(2)

式中： ${{{\boldsymbol{d}}}}_i^l$ ——第i个样本在第l次迭代中的模拟数据；

${\boldsymbol{G}}({\boldsymbol{X}})$ ——正演模型；

${{{\boldsymbol{X}}}}_i^l$ ——模型参数，其中i表示样本编号，l表示迭代更新次数。

针对本研究，模型参数 ${{{{\boldsymbol{X}}}}_i} = {\left[ {{\text{lg(}}{k_{{\mathrm{eff}}}}{\text{)}}} \right]_i}$ ，其中 ${k_{{\mathrm{eff}}}}$ 表示有效渗透率，模拟数据为水头与自然电位数据。

步骤3：更新样本。

${{\boldsymbol{X}}}_{i}^{l+1}={{\boldsymbol{X}}}_{i}^{l}+{{\boldsymbol{C}}}_{{\mathrm{YD}}}({{\boldsymbol{C}}}_{{\mathrm{DD}}}+{\alpha}_{l}{{\boldsymbol{C}}}_{{\mathrm{D}}}{)}^{-1}({{\boldsymbol{d}}}_{{\text{obs}}_{i}}+{{\boldsymbol{d}}}_{i}^{l})$

(3)

式中： ${{{{\boldsymbol{C}}}}_{{\mathrm{YD}}}}$ ——模型参数 ${{{\boldsymbol{X}}}}_{}^l$ 与模拟值 ${{{\boldsymbol{d}}}}^l$ 之间的协方差矩阵；

${{{{\boldsymbol{C}}}}_{{\mathrm{DD}}}}$ ——模拟值的自协方差矩阵；

${{{{\boldsymbol{C}}}}_{\mathrm{D}}}$ ——观测误差的协方差矩阵；

${{{{\boldsymbol{d}}}}_{{\text{obs}}}}$ ——具有协方差 ${{\alpha }_l}{{{{\boldsymbol{C}}}}_{\mathrm{D}}}$ 噪声的扰动观测值。

1.3 直接采样法与集合平滑数据同化框架

ESMDA方法可以获得更好的参数估计效果且计算成本更低，但其仅适用于服从高斯分布的参数场。DS方法作为多点地质统计方法众多算法中的一种，具有重构诸如非高斯参数场等复杂地质模式方面的优势。因此，ESMDA-DS方法结合了上述两种方法各自的优势。

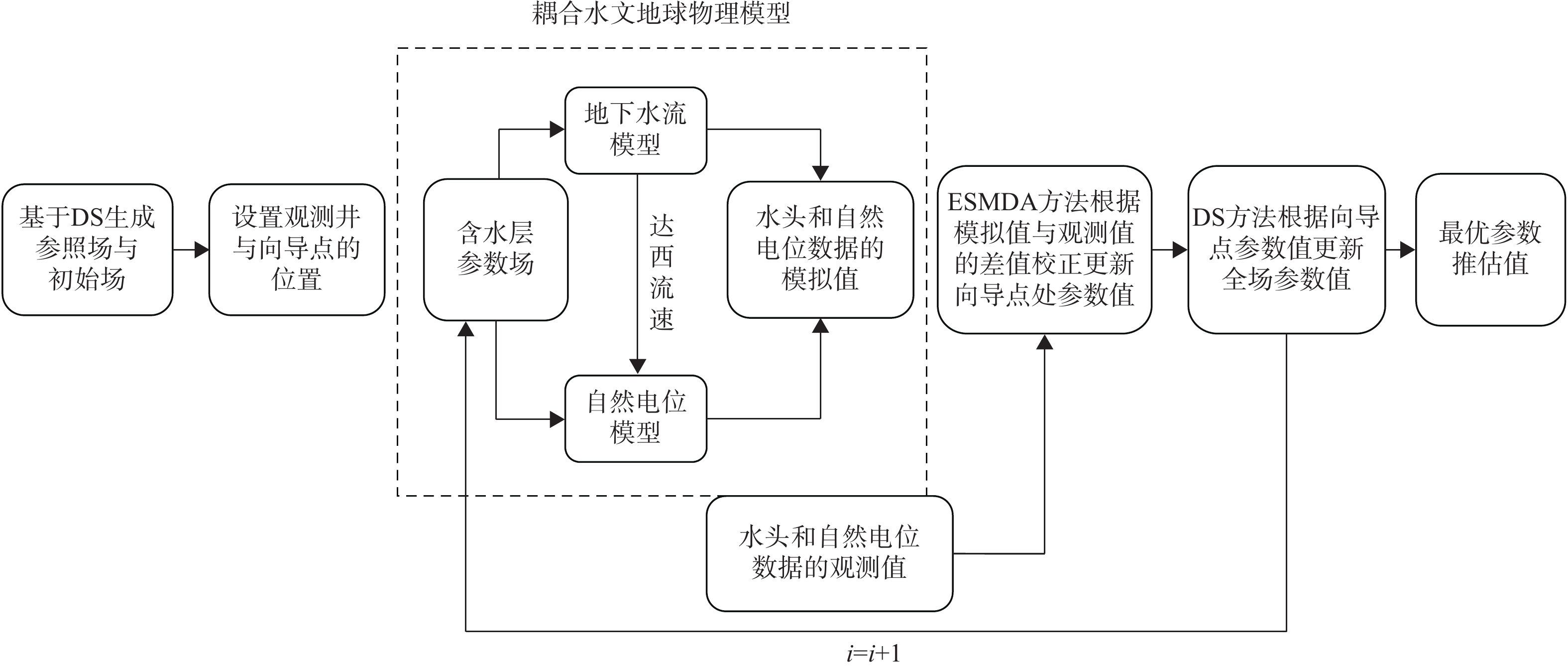
ESMDA-DS方法的步骤流程如图2所示。

图 2. ESMDA-DS数据同化框架

Figure 2. ESMDA-DS data assimilation framework

下载: 全尺寸图片幻灯片

步骤1：基于DS方法生成参照场与初始场。

步骤 2：确定模型中观测井与向导点的数量及位置。

步骤3：在COMSOL软件中耦合地下水流和电场，构建水文地球物理模型，基于参照场运行正演模型获取水头和自然电位的观测数据。

步骤4：基于初始场运行正演模型获得水头和自然电位的模拟数据。ESMDA方法根据模拟值与观测值的差值校正更新向导点处的参数值。

步骤5：基于上一步骤的向导点参数用DS方法更新值更新全场参数值的分布。

步骤6：重复步骤4—步骤6，直至最大迭代次数。

在ESMDA-DS方法中，向导点起关键作用，它将DS和ESMDA方法相互耦合在一起。若没有设置向导点，则ESMDA-DS方法将仅利用DS方法，这样只能保持参数场的非高斯特性，无法融合水头和自然电位等多源观测数据。若模型的所有网格都是向导点，则ESMDA-DS方法将仅利用ESMDA方法，这样只能融合多源观测数据，无法保持参数场的非高斯特性^[27]。

1.4 正演模型

本研究中的正演模型包括地下水流模型和自然电位模型，分别用于获取水头和自然电位数据。自然电位信号的异常是由地下水流运动引起的，当地下水流动时，它会与地下岩石或土壤中的离子发生相互作用，产生电势差。因此，本研究首先求解地下水流模型，然后根据流速求解自然电位模型。

1.4.1 地下水流模型

假定裂隙流运动遵循达西定律，根据质量守恒原理，地下水流运动控制方程为：

$\frac{\partial }{\partial t}({\varepsilon }_{\text{p}}\rho )-\nabla \cdot (\rho {\boldsymbol{u}})=Q$

(4)

式中： ${\varepsilon _{\text{p}}}$ ——孔隙度；

$\rho$ ——孔隙水密度/（kg·m⁻³）；

t——时间/s；

${{{\boldsymbol{u}}}}$ ——流速/（m·s⁻¹）；

$\nabla$ ——梯度算子；

$Q$ ——源汇项/（kg·m⁻³·s⁻¹）。

${{{\boldsymbol{u}}}} = - \frac{{{k_{{\mathrm{eff}}}}}}{\eta }\nabla \rho$

(5)

式中： $\eta$ ——动力黏滞系数/（Pa^.s）。

本文采用COMSOL Multiphysics求解上述水流问题。

1.4.2 自然电位模型

针对自然电位模型，电荷通量可由电流密度（ ${{j}}$ ）表示：

${{j}} = - \sigma \nabla \varphi + {\hat Q_{\mathrm{v}}}{{{\boldsymbol{q}}}}$

(6)

${{{j}}_{{{\mathrm{s}}}}} = {{\hat Q_{\mathrm{v}}}} {{{\boldsymbol{q}}}}$

(7)

${{{j}}_{{{\mathrm{c}}}}} = - \sigma \nabla \varphi$

(8)

式中: ${{{j}}_{{{\mathrm{s}}}}}$ ——欧姆定律推导出的导电电流密度/（A∙m⁻²）；

${{{j}}_{{{\mathrm{c}}}}}$ ——源电流密度/（A∙m⁻²）；

$\sigma$ ——电导率/（S∙m⁻¹）；

$\varphi$ ——电势/V；

${{{\boldsymbol{q}}}}$ ——达西流速/（m∙s⁻¹）， $\boldsymbol{q}=-\mathit{K}\nabla H$ ；

H——水头/m；

K——渗透系数/（m∙s⁻¹）；

${\hat Q _{\mathrm{v}}}$ ——有效电荷密度/（C∙m⁻³）。

由经验公式^{[28 − 29]}与有效对数渗透率建立联系：

$\lg {\hat Q _{\mathrm{v}}} = - 9.2 - 0.82\lg {k_{\rm{eff}}}$

(9)

其中 ${k_{\rm{eff}}}$ 可由有效渗透系数（ ${K_{\rm{eff}}}$ ）转换得出：

${K_{\rm{eff}}} = \rho g{k_{\rm{eff}}}/\eta$

(10)

式中： $g$ ——重力加速度/（m∙s⁻²）。

通过联合式（8）—（10）以及电荷的连续性方程 $（\nabla \cdot j=0）$ ，推导出经典的自然电位方程：

$\nabla \cdot (\sigma \nabla \varphi ) = \nabla \cdot ({\hat Q _{\rm{v}}}{{{\boldsymbol{q}}}})$

(11)

自然电位模型受以下边界条件的约束：

$\varphi = 0\in\varGamma_{\mathrm{ D}}$

(12)

$-{\boldsymbol{n}}\cdot(\sigma\nabla\varphi-\hat{Q}_{\rm{v}})=0\in\varGamma_{\mathrm{N}}$

(13)

式中： $\varGamma_{\mathrm{D}}$ ——狄利克雷（Dirichlet）边界；

$\varGamma_{\mathrm{N}}$ ——纽曼（Neumann）边界；

${{{\boldsymbol{n}}}}$ ——垂直于 $\varGamma_{\mathrm{N}}$ 的法向量。

本文采用COMSOL Multiphysics软件求解自然电位正演问题。

2. 数值算例

本研究通过构建数值算例验证ESMDA-DS方法推估裂隙介质对数渗透率场的效果。模拟区总面积为10000 m²，尺寸为100 m×100 m，z方向的含水层厚度为1 m，裂隙密度为0.0056。研究区内网格均匀划分，网格尺寸为1 m×1 m，数量为10000个。

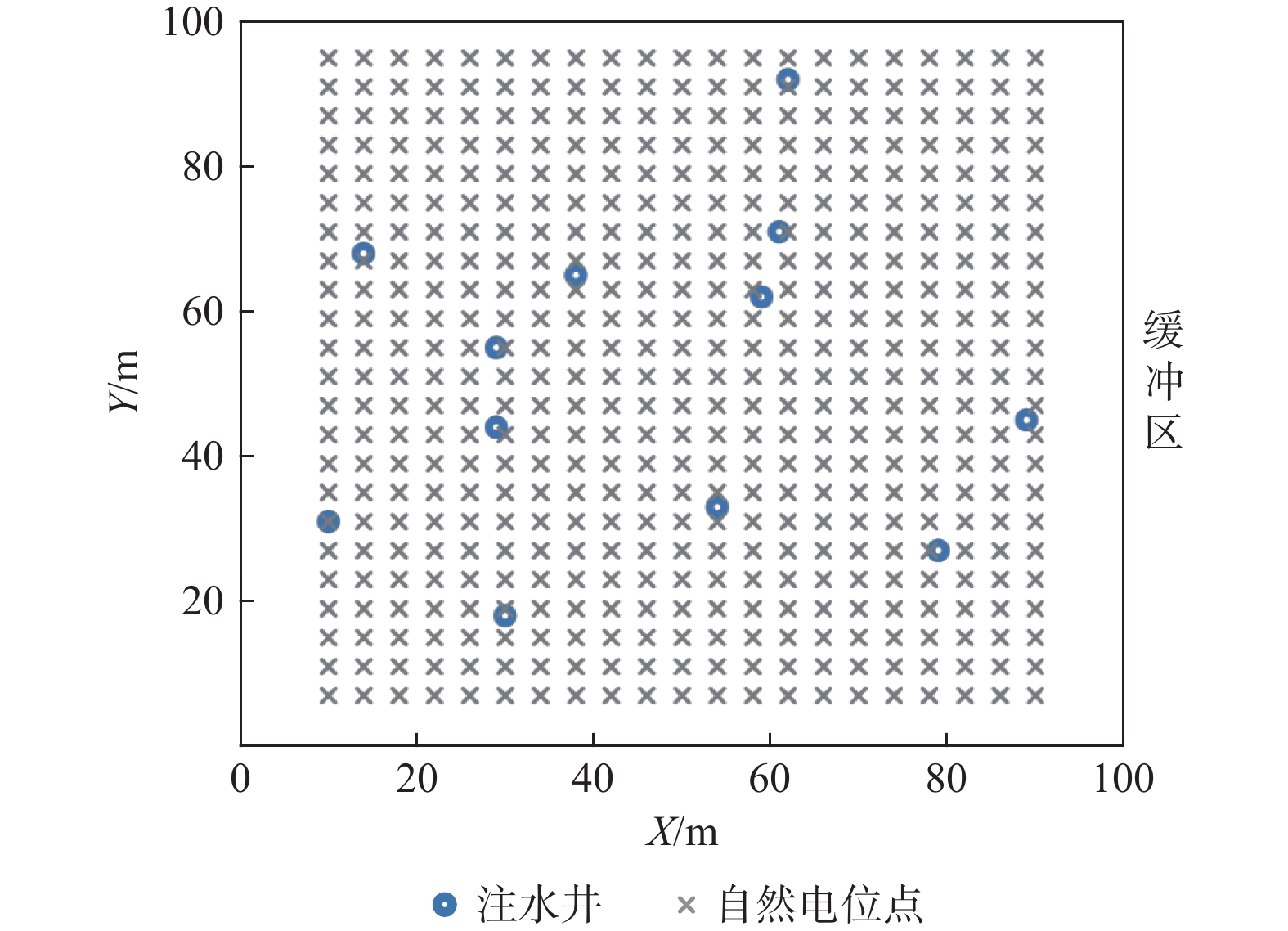
本研究中，为降低边界对模拟结果的影响，模拟区外围设置了600 m×600 m的缓冲区，缓冲区四周设置为给定水头边界/给定电势边界，其边界水头和初始水头均设置为5 m，边界电势和初始电势值均设为0 V。对于地下水流模型，在模拟区内随机设置12口注水井和34 口观测井，其中注水井的注水量为200 m³/d；对于自然电位模型，在模拟区内均匀布设483个自然电位观测点。本研究模拟注水井注水时模拟区内各观测点观测数据（水头、自然电位）的动态变化过程。模拟注水总时长为35 d，每5 d取一次观测数据。12 口注水井依次注水，单口注水井注水时，取35 d的水头观测数据和前15 d的自然电位观测数据，可获取238个水头数据以及1449个自然电位数据，每次模拟共获取2856个水头数据以及17388个自然电位数据。假设水头、自然电位的观测误差均服从高斯分布，均值分别为0 m、0 V，其中水头标准差设置为0.8 m，自然电位的标准差设置为0.2 V^{[36 − 40]}。数值模型设置图如图3所示，模型主要参数设置见表1，缓冲区的主要参数设置与模拟区基质参数保持一致。

图 3. 模型设置

注：模拟区外围设置了600 m×600 m的缓冲区，缓冲区四周设置为5 m的给定水头边界/0 V的给定电势边界。

Figure 3. The setting of groundwater flow model andself-potential model

下载: 全尺寸图片幻灯片

表 1. 地下水流模型和自然电位模型主要参数

Table 1. Parameters in the groundwater flow model and self-potential model

参数	参数值	参数	参数值
网格边长/m	1×1	基质的渗透率/m²	10⁻¹⁵
模型尺寸/m	100×100	缓冲区的渗透率/m²	10⁻¹⁵
初始水头/m	5	初始电位/V	0
流场模拟时间/d	35	电场模拟时间/d	15
流场时间步长/d	5	电场时间步长/d	5
储水系数/Pa⁻¹	6×10⁻⁵	裂隙水的电导率/（S∙m⁻¹）	0.1
裂隙孔隙度	1	基质的电导率/（S∙m⁻¹）	7.5×10⁻⁶
基质孔隙度	0.15	裂隙的相对介电常数	80
裂隙的渗透率/m²	10⁻⁷	基质的相对介电常数	7

| Show Table

DownLoad: CSV

本文共设置8个算例，如表2所示。为研究融合不同类型观测数据对参数推估精度的影响，设置Case1—Case3，分别为仅同化水头数据、仅同化自然电位数据以及同时同化水头和自然电位数据；为探究不同裂隙密度对推估效果的影响，本文在Case1—Case3的基础上分别减小了研究区的裂隙密度设置了Case4—Case6；此外，为分析观测井的数量对推估结果的影响，基于Case3设置了Case7和Case8，依次减少了观测井的数量。

表 2. 算例设置

Table 2. The setting of cases

	向导点数量	观测井数量	注水井数量	裂隙密度	观测数据类型	观测数据量
Case1	1000	34	12	0.00560	H	2856
Case2	1000	34	12	0.00560	SP	17388
Case3	1000	34	12	0.00560	H+SP	20244
Case4	1000	13	10	0.00125	H	910
Case5	1000	13	10	0.00125	SP	14490
Case6	1000	13	10	0.00125	H+SP	15400
Case7	1000	24	12	0.00560	H+SP	19404
Case8	1000	14	12	0.00560	H+SP	18564

| Show Table

DownLoad: CSV

本文引入均方根误差（root mean square error，RMSE），通过计算均方根误差的方法定量分析裂隙介质对数渗透率场的推估精度。RSME数值越小表明参数场的推估效果越好，推估结果越接近参照场。

$I_{\text{RMSE}} = \sqrt {\frac{1}{N}{{\sum\limits_{j = 1}^{N_{\mathrm{e}}} {({{\overline {{{\boldsymbol{Y}}}} }_i} - {{{\boldsymbol{Y}}}}i)^2} }}}$

(14)

式中：I_RMSE——均方根误差；

N —— 网格数量；

N_e——迭代更新的次数；

$\overline {{{{\boldsymbol{Y}}}}_i}$ ——每个网格点推估后的均值；

${{{\boldsymbol{Y}}}}_i$ —— 每个网格点的参照值。

3. 结果

3.1 初始场与参照场的生成

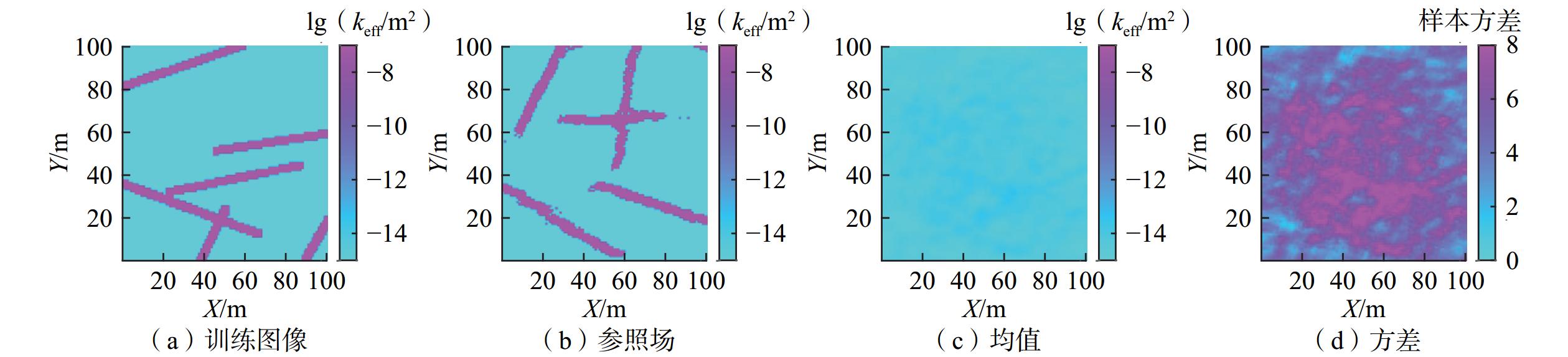
本文采用ESMDA-DS方法进行裂隙介质对数渗透率场的推估。首先利用DS方法基于训练图像（图4a）生成参照场（图4b）；采用DS方法基于训练图像随机生成了200个对数渗透率场^{[26 − 27]}，构成了对数渗透率场的初始参数集合，其中初始场的均值和方差分别如图4（c）、图4（d）所示。在模拟区内随机布设1000个向导点^{[26 − 27]}（图5），利用ESMDA方法同化模拟数据和观测数据，更新向导点的参数值。最后，DS方法根据向导点处的参数值进行插值，推估出全场的对数渗透率分布。

图 4. 训练图像、参照场、初始对数渗透率场均值和初始对数渗透率场方差图

Figure 4. Training images, Reference, mean of lgk_eff, and variance of lgk_eff

下载: 全尺寸图片幻灯片

图 5. 向导点的分布

Figure 5. Distribution of pilot points

下载: 全尺寸图片幻灯片

3.2 裂隙介质对数渗透率场的推估

通过数据同化后的lgk_eff场集合的均值和方差分布评价参数推估的效果。图6为初始场、仅融合水头数据的lgk_eff场（Case1）、仅融合自然电位数据的lgk_eff场（Case2）及同时融合水头和自然电位数据（水文地球物理数据）的lgk_eff场（Case3）的集合均值与方差分布图。

图 6. Case1、Case2及Case3的lgk_eff场集合的均值及方差分布

Figure 6. Mean and variance distribution of the lgk_efffields for Case1, Case2, and Case3

下载: 全尺寸图片幻灯片

Case1仅融合水头数据，虽能大致刻画出裂隙的分布，但同时也明显推估出了部分参照场中并不存在的裂隙，与参照场相比偏差较大。Case2中仅融合自然电位数据，由于地球物理数据推估精度不高，导致交叉裂隙和部分单裂隙部位刻画效果不明显，推估效果较差。相比于Case1和Case2，Case3同时融合水头和自然电位数据（水文地球物理数据）后的lgk_eff场推估效果最好，单裂隙及交叉裂隙的部位均能推估出来，最接近参照场的裂隙分布。同时从3个算例的方差分布图可知，Case3的推估精度明显提高。

为了定量分析lgk_eff场的推估效果，本文计算了Case1—Case3lgk_eff场的I_RMSE ，如表3所示。Case1、Case2及Case3的I_RMSE 分别为2.3377，2.2192，1.9712。相比于Case1和Case2，Case3的I_RMSE 在3个算例中最小。表明相比于融合某一单一类型的观测数据，同时融合水头和自然电位数据的lgk_eff场推估效果最佳。

表 3. Case1、Case2及Case3 lgk_eff场的均方根误差

Table 3. Values of RMSE for Case1, Case2, and Case3 lgk_eff fields

	裂隙密度	融合数据类型	I_RMSE
Case1	0.0056	H	2.3377
Case2	0.0056	SP	2.2192
Case3	0.0056	H+SP	1.9712

| Show Table

DownLoad: CSV

3.3 观测数据的拟合

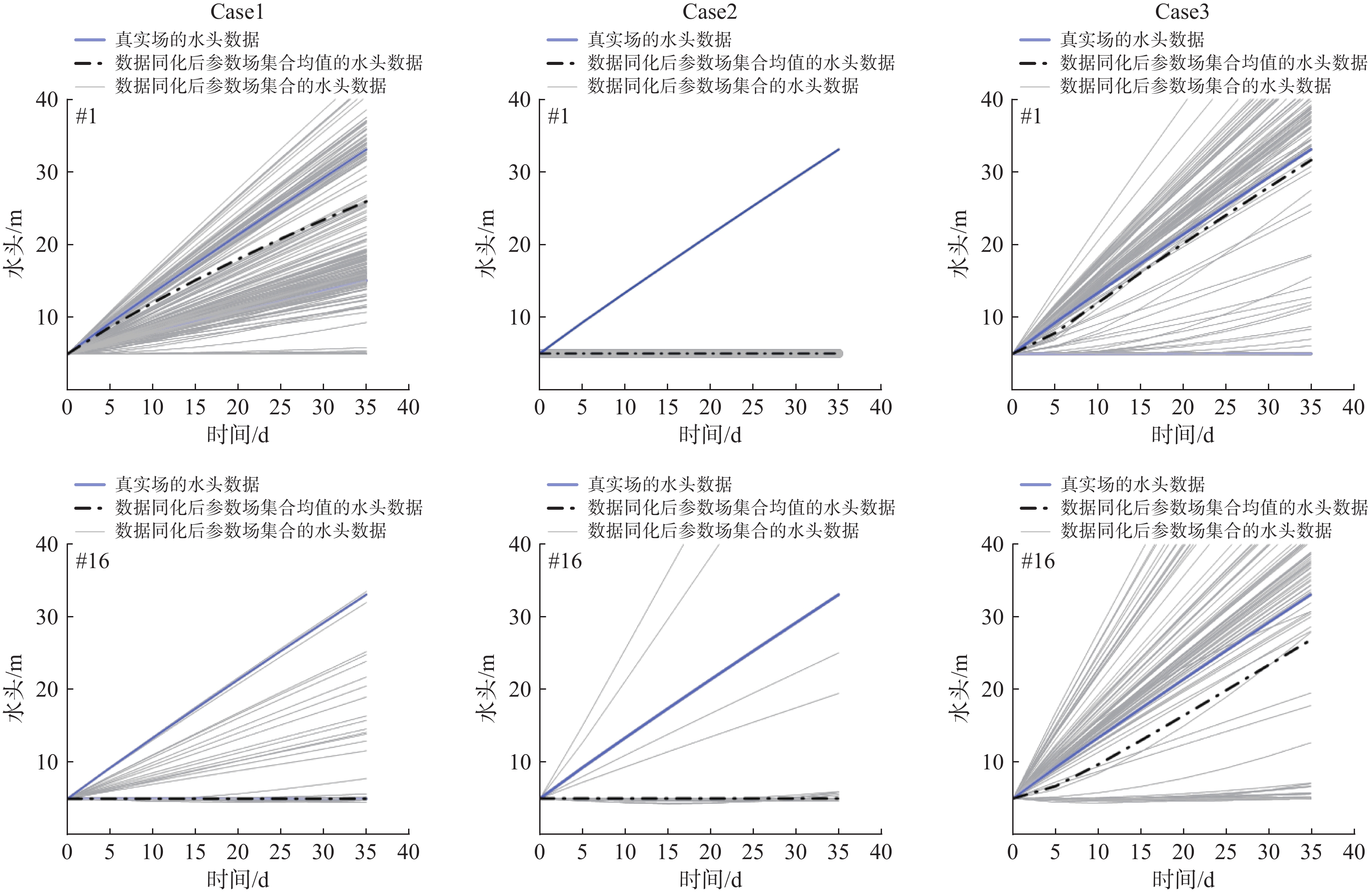
为进一步分析同化3种不同类型的观测数据对参数推估结果的影响，将推估后的参数场代入正演模型进行水头数据拟合^{[12, 27, 35]}。Case1—Case3中均设置34口观测井，其中观测井1（#1）、观测井16（#16）的坐标位置分别为（7,32），（51,8）。图7展示了Case1—Case3中观测井1和观测井16的水头数据拟合情况，总拟合时长为35 d。

图 7. Case1、Case2及Case3水头数据拟合

Figure 7. Hydraulic head data fitting for Case1, Case2, and Case3

下载: 全尺寸图片幻灯片

从观测井1的水头数据拟合结果中可以看出，由于Case1只融合水头数据，其推估精度不高，图中显示lgk_eff场集合均值的水头数据拟合曲线与参照场水头数据拟合曲线走势虽然都呈上升趋势，但两者之间有一定偏差；Case2只融合自然电位数据，lgk_eff场集合均值的水头数据拟合曲线几乎呈水平走势，与参照场拟合曲线呈上升趋势有明显差异。与Case1和Case2相比，Case3同时融合了水头和自然电位观测数据，其推估后lgk_eff场集合均值的水头数据拟合曲线与参照场拟合曲线最为接近，其推估效果最好。

观测井16的水头拟合效果图显示，Case1、Case2推估后lgk_eff场集合均值的水头数据拟合曲线与参照场拟合曲线呈现出不同趋势，前者均呈水平走势，而后者呈上升趋势；Case3的lgk_eff场集合均值的水头拟合曲线更贴近参照场的水头拟合曲线。表明Case3同时融合水头数据和自然电位数据后的lgk_eff场集合更接近参照场的对数渗透率。

然而，图中显示，不管是Case1、Case2还是Case3，lgk_eff场集合的水头拟合曲线仍表现出显著的分散性。这种分散性的主要原因在于裂隙介质的强非均质性，裂隙的渗透率与基质的渗透率相差若干个数量级，具体表现为裂隙介质的渗透率可能在很短距离发生显著变化，使得单次裂隙场实现中同一位置钻孔水头响应差异明显。另外，裂隙长度以及是否交叉都会影响相应的水头响应值。

4. 分析与讨论

4.1 观测数据类型对裂隙含水层参数推估精度的影响

对比分析不同类型的观测数据对裂隙介质对数渗透率场推估效果的影响（图6，表3），通过定量和定性分析可知，3种类型的观测数据（水头、自然电位、水头和自然电位）均可一定程度的推估出裂隙介质对数渗透率场的分布，表明ESMDA-DS方法可有效应用于裂隙介质的参数推估。由于水头数据获取成本较高，其数据量较少，导致其推估误差较大；自然电位数据虽可大量获取，但其推估精度不高。因此，同时融合水头和自然电位数据（水文地球物理数据）的推估效果更优。图7中观测井1和观测井16的水头数据拟合效果进一步验证了Case3的参数推估效果最佳这一结果。表明，相比于融合某一单一数据类型，融合水文地球物理数据能更精准地刻画出裂隙网络的分布。这可能归结于水头和自然电位两类观测值包含非重复的参数信息，增加了有效的观测数据，进行联合同化能得到更准确的参数推估结果。

4.2 裂隙密度对裂隙含水层参数推估精度的影响

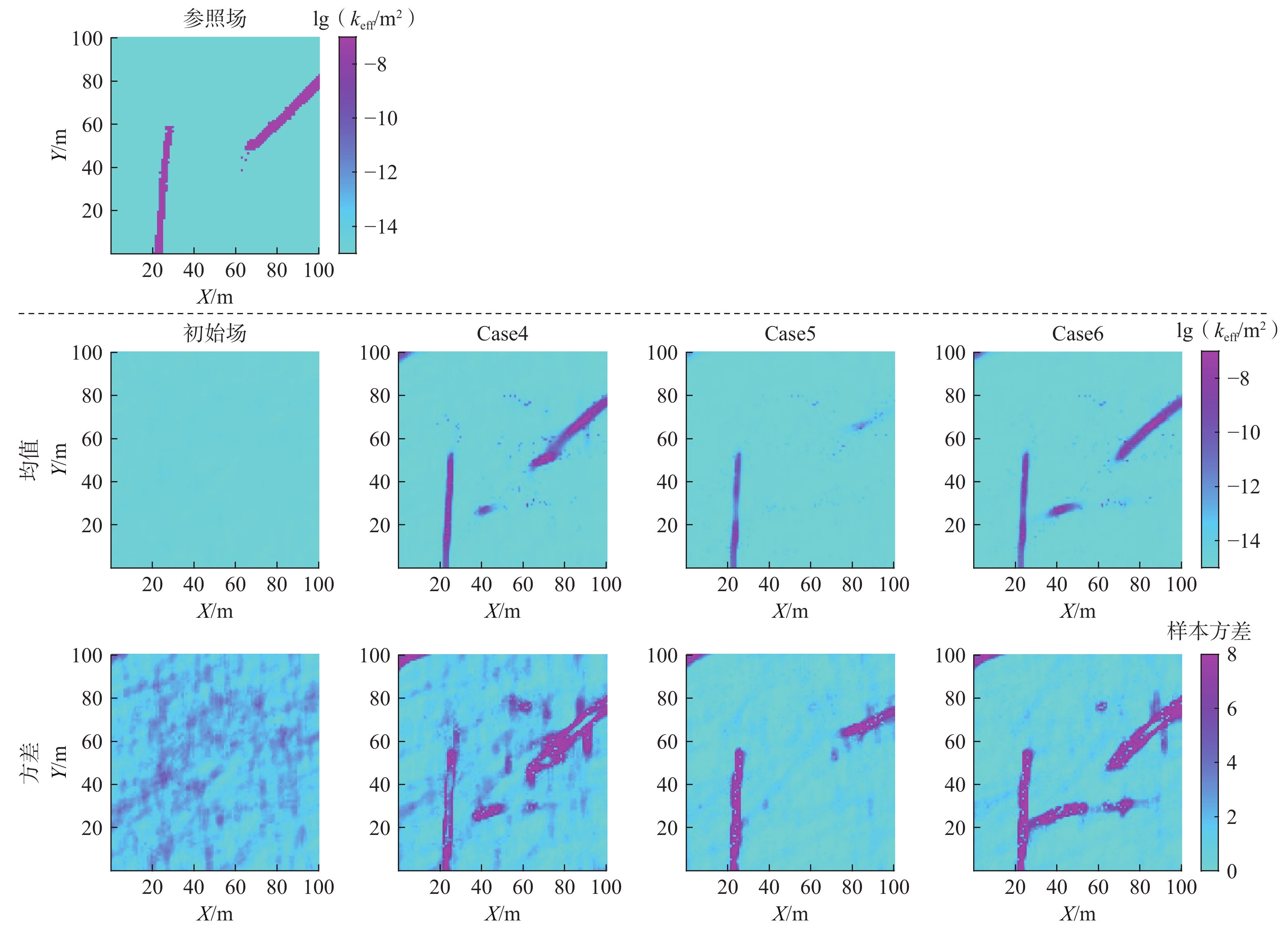
由于野外实际场地的裂隙分布情况较为复杂，为了进一步探究裂隙密度对lgk_eff场推估效果的影响，在Case1—Case3的基础上，分别减小裂隙密度，设置了Case4—Case6。图8为初始场、Case4、Case5及Case6的lgk_eff场的集合均值与方差分布图。

图 8. Case4、Case5及Case6的lgk_eff场集合的均值及方差分布

Figure 8. Distributions of the mean and variance of lgk_eff fields for Case4, Case5, and Case6

下载: 全尺寸图片幻灯片

图中显示，Case4中，融合水头数据基本能够推估出裂隙的分布；Case5只融合自然电位数据推估效果相比于Case4较差，右上角的单裂隙推估效果不显著；Case6同时融合水头数据和自然电位数据的推估效果最佳，能有效识别出2条裂隙，相较于Case4和Case5，Case6推估精度最高。

针对本研究，对比图6与图8中的算例可以看出，Case4、Case5及Case6的推估效果分别优于Case1、Case2及Case3；同样地对比Case4—Case6的I_RMSE （表4）发现，Case4、Case5及Case6的I_RMSE 分别小于Case1、Case2及Case3的I_RMSE ，说明当融合同种观测数据类型时，随着裂隙密度减小，算例的推估效果逐渐变好且误差随之变小。

表 4. Case4、Case5及Case6 lgk_eff场的均方根误差

Table 4. Values of RMSE for Case4, Case5, and Case6 lgk_eff fields

	裂隙密度	融合数据类型	I_RMSE
Case4	0.00125	H	1.1621
Case5	0.00125	SP	1.3648
Case6	0.00125	H+SP	1.1488

| Show Table

DownLoad: CSV

此外，对比表3与表4可以看出，不论裂隙密度大小，同时融合水头和自然电位数据（水文地球物理数据）的lgk_eff场的I_RMSE 均为最小，进一步说明了多种类型观测数据联合推估的优势。

4.3 观测井数量对裂隙含水层参数推估精度的影响

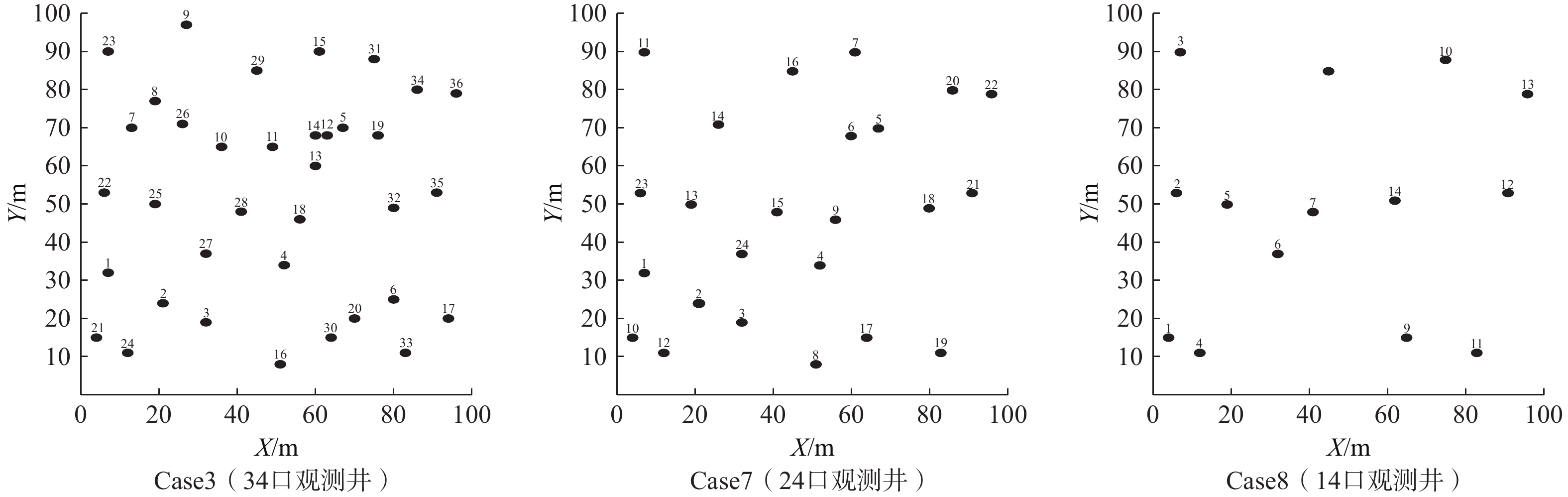
由于传统的野外裂隙识别方法主要是钻孔采样，获取观测数据成本较高。探究观测井数量对参数推估精度的影响，将会给实际研究中观测井数量的合理选择提供重要依据。本文在Case3的基础上，增加两组算例Case7、Case8，其他条件均不变，依次减少观测的数量。3个算例的观测井均随机分布，数量分别为34，24，14（图9）。

图 9. Case3、Case7及Case8观测井分布

Figure 9. Distribution of observation wells for Case3, Case7, and Case8

下载: 全尺寸图片幻灯片

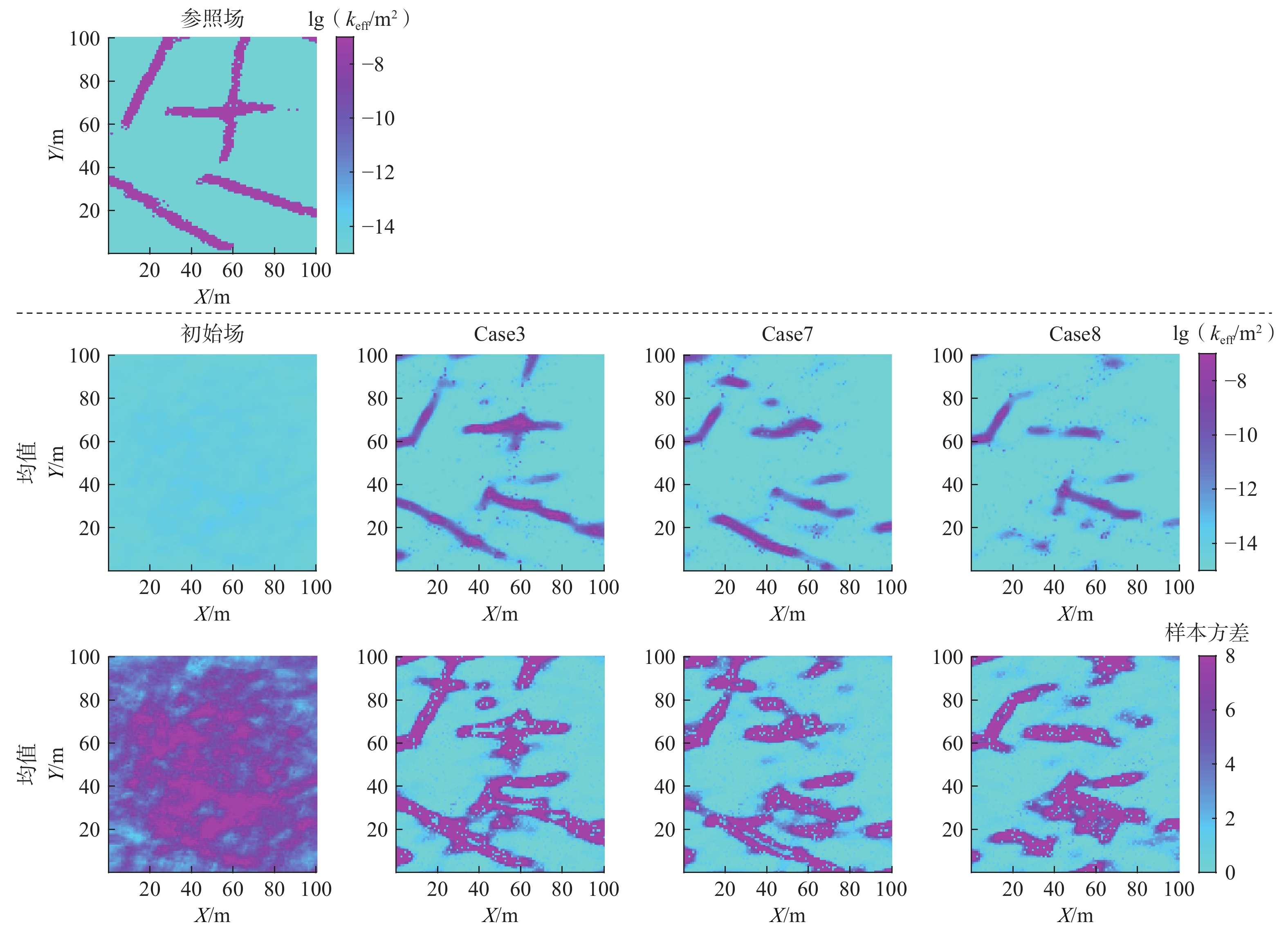
图10是Case3、Case7及Case8的lgk_eff场的集合均值与方差图。可以看出Case8的推估效果最差，仅刻画出少量的裂隙且精度不高；其次是Case7，与Case8相比推估精度有显著的提高，但交叉裂隙部分刻画效果仍不理想；Case3的推估效果表现最优，基本刻画出了与参照场相近的裂隙分布。

图 10. Case3、Case7及Case8的lgk_eff场集合的均值、方差分布

Figure 10. Distributions of Mean and variance of the lgk_efffields for Case3, Case7, and Case8

下载: 全尺寸图片幻灯片

表5为Case3、Case7及Case8对应的I_RMSE ，其定量计算结果与图10分析结果相符。Case3的观测井数量为34口，其I_RMSE 为1.9712；与Case3相比，Case7的观测井数量减少至24口，其I_RMSE 增大为2.3435；而Case8的观测井数量继续降低至14口，则I_RMSE 继续增大到2.5092。结果显示当观测井数量逐渐减少时，I_RMSE 逐渐增大。

表 5. Case3、Case7及Case8 lgk_eff场的均方根误差

Table 5. Values of RMSE for Case3, Case7, and Case8 lgk_eff fields

	观测井数量	融合数据类型	I_RMSE
Case3	34	H+SP	1.9712
Case7	24	H+SP	2.3435
Case8	14	H+SP	2.5092

| Show Table

DownLoad: CSV

通过上述定性与定量分析可知，随着观测井数量的增加，I_RMSE 逐渐减小，误差降低，裂隙介质的对数渗透率的推估效果也逐渐得到提高。

5. 结论

（1）ESMDA-DS方法既保留了DS方法能够保持参数场的非高斯特性又结合了ESMDA可以融合多源数据的优势，通过设置多组算例，验证了基于ESMDA-DS方法同时融合水头和水文地球物理数据可有效地刻画裂隙网络的分布。

（2）比较3种观测数据类型，相比于某一单一类型的数据类型，同时融合水头和自然电位数据（水文地球物理数据），即融合多源数据能更精确地推估出裂隙介质的参数场。后续研究中可考虑融合更多类型的观测数据，如其它地球物理数据、温度数据等。

（3）裂隙密度、观测井的数量均会对裂隙介质参数场的推估效果产生影响。在本研究算例中，裂隙介质参数场的推估精度会随着裂隙密度的减小以及观测井数量的增加而提高，使参数场的推估结果与真实场更接近。在实际研究中，观测井的数量将会直接影响计算成本。因此，需要权衡计算成本与参数推估效果之间的关系。另外，如何合理地选择观测井的数量也值得在后续研究中进一步探讨。

图 1 DS方法主要步骤流程图

Figure 1.

下载: 全尺寸图片幻灯片

图 2 ESMDA-DS数据同化框架

Figure 2.

下载: 全尺寸图片幻灯片

图 3 模型设置

Figure 3.

下载: 全尺寸图片幻灯片

图 4 训练图像、参照场、初始对数渗透率场均值和初始对数渗透率场方差图

Figure 4.

下载: 全尺寸图片幻灯片

图 5 向导点的分布

Figure 5.

下载: 全尺寸图片幻灯片

图 6 Case1、Case2及Case3的lgk_eff场集合的均值及方差分布

Figure 6.

下载: 全尺寸图片幻灯片

图 7 Case1、Case2及Case3水头数据拟合

Figure 7.

下载: 全尺寸图片幻灯片

图 8 Case4、Case5及Case6的lgk_eff场集合的均值及方差分布

Figure 8.

下载: 全尺寸图片幻灯片

图 9 Case3、Case7及Case8观测井分布

Figure 9.

下载: 全尺寸图片幻灯片

图 10 Case3、Case7及Case8的lgk_eff场集合的均值、方差分布

Figure 10.

下载: 全尺寸图片幻灯片

表 1 地下水流模型和自然电位模型主要参数

Table 1. Parameters in the groundwater flow model and self-potential model

参数	参数值	参数	参数值
网格边长/m	1×1	基质的渗透率/m²	10⁻¹⁵
模型尺寸/m	100×100	缓冲区的渗透率/m²	10⁻¹⁵
初始水头/m	5	初始电位/V	0
流场模拟时间/d	35	电场模拟时间/d	15
流场时间步长/d	5	电场时间步长/d	5
储水系数/Pa⁻¹	6×10⁻⁵	裂隙水的电导率/（S∙m⁻¹）	0.1
裂隙孔隙度	1	基质的电导率/（S∙m⁻¹）	7.5×10⁻⁶
基质孔隙度	0.15	裂隙的相对介电常数	80
裂隙的渗透率/m²	10⁻⁷	基质的相对介电常数	7

下载: 导出CSV

表 2 算例设置

Table 2. The setting of cases

	向导点数量	观测井数量	注水井数量	裂隙密度	观测数据类型	观测数据量
Case1	1000	34	12	0.00560	H	2856
Case2	1000	34	12	0.00560	SP	17388
Case3	1000	34	12	0.00560	H+SP	20244
Case4	1000	13	10	0.00125	H	910
Case5	1000	13	10	0.00125	SP	14490
Case6	1000	13	10	0.00125	H+SP	15400
Case7	1000	24	12	0.00560	H+SP	19404
Case8	1000	14	12	0.00560	H+SP	18564

下载: 导出CSV

表 3 Case1、Case2及Case3 lgk_eff场的均方根误差

Table 3. Values of RMSE for Case1, Case2, and Case3 lgk_eff fields

	裂隙密度	融合数据类型	I_RMSE
Case1	0.0056	H	2.3377
Case2	0.0056	SP	2.2192
Case3	0.0056	H+SP	1.9712

下载: 导出CSV

表 4 Case4、Case5及Case6 lgk_eff场的均方根误差

Table 4. Values of RMSE for Case4, Case5, and Case6 lgk_eff fields

	裂隙密度	融合数据类型	I_RMSE
Case4	0.00125	H	1.1621
Case5	0.00125	SP	1.3648
Case6	0.00125	H+SP	1.1488

下载: 导出CSV

表 5 Case3、Case7及Case8 lgk_eff场的均方根误差

Table 5. Values of RMSE for Case3, Case7, and Case8 lgk_eff fields

	观测井数量	融合数据类型	I_RMSE
Case3	34	H+SP	1.9712
Case7	24	H+SP	2.3435
Case8	14	H+SP	2.5092

下载: 导出CSV

参考文献(40)

[1]	LIU Longcheng,MENG Shuo,LI Chunguang. A new analytical solution of contaminant transport along a single fracture connected with porous matrix and its time domain random walk algorithm[J]. Journal of Hydrology,2022,610(1):127828.
[2]	JI Jiayan,SONG Xianzhi,SONG Guofeng,et al. Study on fracture evolution model of the enhanced geothermal system under thermal-hydraulic-chemical-deformation coupling[J]. Energy,2023,269:126604. doi: 10.1016/j.energy.2022.126604
[3]	张烈辉,贾鸣,张芮菡,等. 裂缝性油藏离散裂缝网络模型与数值模拟[J]. 西南石油大学学报(自然科学版),2017,39(3):121 − 127. [ZHANG Liehui,JIA Ming,ZHANG Ruihan,et al. Discrete fracture network modeling and numerical simulation of fractured reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition),2017,39(3):121 − 127. (in Chinese with English abstract)] ZHANG Liehui, JIA Ming, ZHANG Ruihan, et al. Discrete fracture network modeling and numerical simulation of fractured reservoirs[J]. Journal of Southwest Petroleum University （Science & Technology Edition）, 2017, 39（3）: 121 − 127. （in Chinese with English abstract）
[4]	石鸿蕾,郝奇琛,邵景力,等. 基于多源数据的弱透水层水文地质参数反演研究——以呼和浩特盆地某淤泥层为例[J]. 水文地质工程地质,2021,48(2):1 − 7. [SHI Honglei,HAO Qichen,SHAO Jingli,et al. Research on hydrogeological parameter inversion of an aquitard based on multi-source data:A case study of a silt layer in the Hohhot Basin[J]. Hydrogeology & Engineering Geology,2021,48(2):1 − 7. (in Chinese with English abstract)] SHI Honglei, HAO Qichen, SHAO Jingli, et al. Research on hydrogeological parameter inversion of an aquitard based on multi-source data: A case study of a silt layer in the Hohhot Basin[J]. Hydrogeology & Engineering Geology, 2021, 48（2）: 1 − 7. （in Chinese with English abstract）
[5]	吴延浩,江思珉,吴自军. 地下水污染强度及渗透系数场的反演识别研究[J]. 水文地质工程地质,2023,50(4):193 − 203. [WU Yanhao,JIANG Simin,WU Zijun. Identification of groundwater pollution intensity and hydraulic conductivity field[J]. Hydrogeology & Engineering Geology,2023,50(4):193 − 203. (in Chinese with English abstract)] WU Yanhao, JIANG Simin, WU Zijun. Identification of groundwater pollution intensity and hydraulic conductivity field[J]. Hydrogeology & Engineering Geology, 2023, 50（4）: 193 − 203. （in Chinese with English abstract）
[6]	陈梦迪,姜振蛟,霍晨琛. 考虑矿层渗透系数非均质性和不确定性的砂岩型铀矿地浸采铀过程随机模拟与分析[J]. 水文地质工程地质,2023,50(2):63 − 72. [CHEN Mengdi,JIANG Zhenjiao,HUO Chenchen. Stochastic modeling of in situ sandstone-type uranium leaching in response to uncertain and heterogeneous hydraulic conductivity[J]. Hydrogeology & Engineering Geology,2023,50(2):63 − 72. (in Chinese with English abstract)] CHEN Mengdi, JIANG Zhenjiao, HUO Chenchen. Stochastic modeling of in situ sandstone-type uranium leaching in response to uncertain and heterogeneous hydraulic conductivity[J]. Hydrogeology & Engineering Geology, 2023, 50（2）: 63 − 72. （in Chinese with English abstract）
[7]	KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering,1960,82(1):35 − 45. doi: 10.1115/1.3662552
[8]	VAN LEEUWEN P J,EVENSEN G. Data assimilation and inverse methods in terms of a probabilistic formulation[J]. Monthly Weather Review,1996,124(12):2898 − 2913. doi: 10.1175/1520-0493(1996)124<2898:DAAIMI>2.0.CO;2
[9]	ZHANG Jiangjiang,LIN Guang,LI Weixuan,et al. An iterative local updating ensemble smoother for estimation and uncertainty assessment of hydrologic model parameters with multimodal distributions[J]. Water Resources Research,2018,54(3):1716 − 1733. doi: 10.1002/2017WR020906
[10]	EVENSEN G. The Ensemble Kalman Filter:Theoretical formulation and practical implementation[J]. Ocean Dynamics,2003,53(4):343 − 367. doi: 10.1007/s10236-003-0036-9
[11]	康学远,施小清,邓亚平,等. 基于EnKF融合地球物理数据刻画含水层非均质性[J]. 水科学进展,2018,29(1):40 − 49. [KANG Xueyuan,SHI Xiaoqing,DENG Yaping,et al. Assimilation of hydrogeophysical data for the characterization of subsurface heterogeneity using Ensemble Kalman Filter (EnKF)[J]. Advances in Water Science,2018,29(1):40 − 49. (in Chinese with English abstract)] KANG Xueyuan, SHI Xiaoqing, DENG Yaping, et al. Assimilation of hydrogeophysical data for the characterization of subsurface heterogeneity using Ensemble Kalman Filter （EnKF）[J]. Advances in Water Science, 2018, 29（1）: 40 − 49. （in Chinese with English abstract）
[12]	兰天,康学远,施小清,等. 基于EnKF综合水头和浓度观测数据推估地下水流模型参数[J]. 水文地质工程地质,2017,44(5):6 − 13. [LAN Tian,KANG Xueyuan,SHI Xiaoqing,et al. Joint assimilation of heads and concentrations for estimating parameters of groundwater flow models using the Ensemble Kalman Filter[J]. Hydrogeology & Engineering Geology,2017,44(5):6 − 13. (in Chinese with English abstract)] LAN Tian, KANG Xueyuan, SHI Xiaoqing, et al. Joint assimilation of heads and concentrations for estimating parameters of groundwater flow models using the Ensemble Kalman Filter[J]. Hydrogeology & Engineering Geology, 2017, 44（5）: 6 − 13. （in Chinese with English abstract）
[13]	CHEN Yan,OLIVER D S. Ensemble randomized maximum likelihood method as an iterative ensemble smoother[J]. Mathematical Geosciences,2012,44(1):1 − 26. doi: 10.1007/s11004-011-9376-z
[14]	夏传安,王浩,简文彬. 基于相关性局域化迭代集合平滑反演渗透系数场[J]. 水文地质工程地质,2024,51(1):12 − 21. [XIA Chuanan,WANG Hao,JIAN Wenbin. Estimation of conductivity fields by using a correlation-based localization scheme of iterative ensemble smoother[J]. Hydrogeology & Engineering Geology,2024,51(1):12 − 21. (in Chinese)] XIA Chuanan, WANG Hao, JIAN Wenbin. Estimation of conductivity fields by using a correlation-based localization scheme of iterative ensemble smoother[J]. Hydrogeology & Engineering Geology, 2024, 51（1）: 12 − 21. （in Chinese）
[15]	EMERICK A,REYNOLDS A. Ensemble smoother with multiple data assimilation[J]. Computers & Geosciences,2013,55(3):3 − 15.
[16]	周念清,张瑞城,江思珉,等. ES-MDA算法融合ERT数据联合反演地下水污染源与含水层参数[J]. 南水北调与水利科技(中英文),2022,20(3):478 − 486. [ZHOU Nianqing,ZHANG Ruicheng,JIANG Simin,et al. Joint inversion of contaminant source and aquifer parameters by assimilating ERT data with the ES-MDA algorithm[J]. South-to-North Water Transfers and Water Science & Technology,2022,20(3):478 − 486. (in Chinese with English abstract)] ZHOU Nianqing, ZHANG Ruicheng, JIANG Simin, et al. Joint inversion of contaminant source and aquifer parameters by assimilating ERT data with the ES-MDA algorithm[J]. South-to-North Water Transfers and Water Science & Technology, 2022, 20（3）: 478 − 486. （in Chinese with English abstract）
[17]	HAN Zheng,KANG Xueyuan,WU Jichun,et al. Characterization of the non-Gaussian hydraulic conductivity field via deep learning-based inversion of hydraulic-head and self-potential data[J]. Journal of Hydrology,2022,610(11):127830.
[18]	CUI Fan,BAO Jichao,CAO Zhendan,et al. Soil hydraulic parameters estimation using ground penetrating radar data via ensemble smoother with multiple data assimilation[J]. Journal of Hydrology,2020,583(12):124552.
[19]	CAMPORESE M,CASSIANI G,DEIANA R,et al. Coupled and uncoupled hydrogeophysical inversions using ensemble Kalman filter assimilation of ERT-monitored tracer test data[J]. Water Resources Research,2015,51(5):3277 − 3291. doi: 10.1002/2014WR016017
[20]	JARDANI A,REVIL A,BOLÈVE A,et al. Tomography of the Darcy velocity from self-potential measurements[J]. Geophysical Research Letters,2007,34(12):L24403.
[21]	STREBELLE S,JOURNEL A. Reservoir modeling using multiple-point statistics[C]//Proceedings of SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers,2001:1-11.
[22]	STREBELLE S. Conditional simulation of complex geological structures using multiple-point statistics[J]. Mathematical Geology,2002,34(1):1 − 21. doi: 10.1023/A:1014009426274
[23]	ARPAT G B,CAERS J. Conditional simulation with patterns[J]. Mathematical Geology,2007,39(2):177 − 203. doi: 10.1007/s11004-006-9075-3
[24]	ZHANG Tuanfeng,SWITZER P,JOURNEL A. Filter-based classification of training image patterns for spatial simulation[J]. Mathematical Geology,2006,38(1):63 − 80. doi: 10.1007/s11004-005-9004-x
[25]	MARIETHOZ G,RENARD P,STRAUBHAAR J. The direct sampling method to perform multiple-point geostatistical simulations[J]. Water Resources Research,2010,46(11):W11536.
[26]	CAO Zhendan,LI Liangping,CHEN Kang. Bridging iterative Ensemble Smoother and multiple-point geostatistics for better flow and transport modeling[J]. Journal of Hydrology,2018,565:411 − 421. doi: 10.1016/j.jhydrol.2018.08.023
[27]	宗成元,康学远,施小清,等. 基于多点地质统计与集合平滑数据同化方法识别非高斯渗透系数场[J]. 水文地质工程地质,2020,47(2):1 − 8. [ZONG Chengyuan,KANG Xueyuan,SHI Xiaoqing,et al. Characterization of non-Gaussian hydraulic conductivity fields using multiple-point geostatistics and ensemble smoother with multiple data assimilation method[J]. Hydrogeology & Engineering Geology,2020,47(2):1 − 8. (in Chinese with English abstract)] ZONG Chengyuan, KANG Xueyuan, SHI Xiaoqing, et al. Characterization of non-Gaussian hydraulic conductivity fields using multiple-point geostatistics and ensemble smoother with multiple data assimilation method[J]. Hydrogeology & Engineering Geology, 2020, 47（2）: 1 − 8. （in Chinese with English abstract）
[28]	JOUGNOT D,LINDE N,REVIL A,et al. Derivation of soil-specific streaming potential electrical parameters from hydrodynamic characteristics of partially saturated soils[J]. Vadose Zone Journal,2012,11(1):272 − 286.
[29]	REVIL A. Transport of water and ions in partially water-saturated porous media. Part 1. Constitutive equations[J]. Advances in Water Resources,2017,103:119 − 138. doi: 10.1016/j.advwatres.2016.02.006
[30]	李华,王东辉,张伟,等. 地球物理探测技术在成都市浅表地质结构调查中的应用研究[J]. 中国地质,2022,49(5):1438 − 1457. [LI Hua,WANG Donghui,ZHANG Wei,et al. Application research of geophysical exploration technology in the investigation of shallow geological structure in Chengdu[J]. Geology in China,2022,49(5):1438 − 1457. (in Chinese with English abstract)] LI Hua, WANG Donghui, ZHANG Wei, et al. Application research of geophysical exploration technology in the investigation of shallow geological structure in Chengdu[J]. Geology in China, 2022, 49（5）: 1438 − 1457. （in Chinese with English abstract）
[31]	赵全升,孔智涵,胡舒娅,等. 柴达木盆地马海盐湖地下卤水地球物理探测及应用[J]. 吉林大学学报(地球科学版),2023,53(5):1560 − 1572. [Zhao Quansheng,Kong Zhihan,Hu Shuya, et al. Geophysical exploration and application of underground brine of Mahai Salt Lake in Qaidam Basin[J]. Journal of Jilin University (Earth Science Edition),2023,53(5):1560 − 1572. (in Chinese with English abstract)] Zhao Quansheng, Kong Zhihan, Hu Shuya, et al. Geophysical exploration and application of underground brine of Mahai Salt Lake in Qaidam Basin[J]. Journal of Jilin University (Earth Science Edition), 2023, 53（5）: 1560 − 1572. （in Chinese with English abstract）
[32]	丁万奇,马振乾,祖自银,等. 基于分形维数的巷道围岩裂隙演化规律研究[J]. 煤田地质与勘探,2021,49(3):167 − 174. [DING Wanqi,MA Zhenqian,ZU Ziyin,et al. Research on the evolution law of roadway surrounding rock fissure based on fractal dimension[J]. Coal Geology & Exploration,2021,49(3):167 − 174. (in Chinese with English abstract)] DING Wanqi, MA Zhenqian, ZU Ziyin, et al. Research on the evolution law of roadway surrounding rock fissure based on fractal dimension[J]. Coal Geology & Exploration, 2021, 49（3）: 167 − 174. （in Chinese with English abstract）
[33]	WANG Libing. Modeling complex reservoir geometries with multiple-point statistics[J]. Mathematical Geology,1996,28(7):895 − 907. doi: 10.1007/BF02066007
[34]	ZHANG Dailu,ZHANG Hongbing,REN Quan,et al. A modified method of multiple point geostatistics for spatial simulation of sedimentary facies for carbonate reservoirs[J]. Journal of Applied Geophysics,2023,215:105112. doi: 10.1016/j.jappgeo.2023.105112
[35]	王鸣川,商晓飞,段太忠. 多点地质统计学建模中训练图像建立方法综述[J]. 高校地质学报,2022,28(1):96 − 103. [WANG Mingchuan,SHANG Xiaofei,DUAN Taizhong. A review of the establishment methods of training image in multiple-point statistics modeling[J]. Geological Journal of China Universities,2022,28(1):96 − 103. (in Chinese with English abstract)] WANG Mingchuan, SHANG Xiaofei, DUAN Taizhong. A review of the establishment methods of training image in multiple-point statistics modeling[J]. Geological Journal of China Universities, 2022, 28（1）: 96 − 103. （in Chinese with English abstract）
[36]	NAN Tongchao,WU Jichun. Groundwater parameter estimation using the ensemble Kalman filter with localization[J]. Hydrogeology Journal,2011,19(3):547 − 561. doi: 10.1007/s10040-010-0679-9
[37]	LEE J,KITANIDIS P K. Large-scale hydraulic tomography and joint inversion of head and tracer data using the Principal Component Geostatistical Approach (PCGA)[J]. Water Resources Research,2014,50(7):5410 − 5427. doi: 10.1002/2014WR015483
[38]	兰天. 基于改进PCM方法反演非高斯水文地质参数[D]. 南京:南京大学,2020. [LAN Tian. Inversion of Non-Gaussian Hydrogeological Parameters by Modified Probability Conditioning Method[D]. Nanjing:Nanjing University,2020. (in Chinese with English abstract)] LAN Tian. Inversion of Non-Gaussian Hydrogeological Parameters by Modified Probability Conditioning Method[D]. Nanjing: Nanjing University, 2020. （in Chinese with English abstract）
[39]	HUANG Xiang,ANDREWS C B,LIU Jie,et al. Assimilation of temperature and hydraulic gradients for quantifying the spatial variability of streambed hydraulics[J]. Water Resources Research,2016,52(8):6419 − 6439. doi: 10.1002/2015WR018408
[40]	ZHAN Chuanjun,DAI Zhenxue,SOLTANIAN M R,et al. Data-worth analysis for heterogeneous subsurface structure identification with a stochastic deep learning framework[J]. Water Resources Research,2022,58(11):e2022WR033241. doi: 10.1029/2022WR033241

施引文献

期刊类型引用(1)

1.	戴君一，王礼春，孙晓林. 裂隙扩张及惯性效应共同作用下裂隙中非达西渗流模拟研究. 水文地质工程地质. 2025(02): 44-52 . 本站查看

其他类型引用(0)

资源附件(0)

访问统计

图(10)

表(5)

计量

文章访问数: 702
PDF下载数: 30
施引文献: 1

1. 研究方法
1.1 直接采样法
1.2 集合平滑数据同化方法
1.3 直接采样法与集合平滑数据同化框架
1.4 正演模型
2. 数值算例
3. 结果
3.1 初始场与参照场的生成
3.2 裂隙介质对数渗透率场的推估
3.3 观测数据的拟合
4. 分析与讨论
4.1 观测数据类型对裂隙含水层参数推估精度的影响
4.2 裂隙密度对裂隙含水层参数推估精度的影响
4.3 观测井数量对裂隙含水层参数推估精度的影响
5. 结论

基于集合平滑数据同化与直接采样法融合水文地球物理数据刻画裂隙网络分布

合肥工业大学资源与环境工程学院，安徽 合肥 230009

作者简介: 焦婷婷（1996—），女，硕士研究生，主要从事地下水数值模拟研究。E-mail：2021110687@mail.hfut.edu.cn

通讯作者: 邓亚平（1989—），女，博士，讲师，主要从事水文地球物理和水文地质参数反演等领域的研究。E-mail：dengyaping@hfut.edu.cn

Characterizing fracture networks by integrating hydrogeophysical data based on the ESMDA-DS method

School of Resources and Environmental Engineering, Hefei University of Technology, Hefei, Anhui 230009, China

Corresponding author: DENG Yaping, dengyaping@hfut.edu.cn

1. 研究方法

1.1 直接采样法

1.2 集合平滑数据同化方法

1.3 直接采样法与集合平滑数据同化框架

1.4 正演模型

1.4.1 地下水流模型

1.4.2 自然电位模型

2. 数值算例

3. 结果

3.1 初始场与参照场的生成

3.2 裂隙介质对数渗透率场的推估

3.3 观测数据的拟合

4. 分析与讨论

4.1 观测数据类型对裂隙含水层参数推估精度的影响

4.2 裂隙密度对裂隙含水层参数推估精度的影响

4.3 观测井数量对裂隙含水层参数推估精度的影响

5. 结论

期刊类型引用(1)

其他类型引用(0)

计量

出版历程

目录

1. 研究方法

1.1 直接采样法

1.2 集合平滑数据同化方法

1.3 直接采样法与集合平滑数据同化框架

1.4 正演模型

1.4.1 地下水流模型

1.4.2 自然电位模型

2. 数值算例

3. 结果

3.1 初始场与参照场的生成

3.2 裂隙介质对数渗透率场的推估

3.3 观测数据的拟合

4. 分析与讨论

4.1 观测数据类型对裂隙含水层参数推估精度的影响

4.2 裂隙密度对裂隙含水层参数推估精度的影响

4.3 观测井数量对裂隙含水层参数推估精度的影响

5. 结论

合肥工业大学资源与环境工程学院，安徽合肥　230009

School of Resources and Environmental Engineering, Hefei University of Technology, Hefei, Anhui　230009, China