Processing math: 100%
2025年4月11日 星期五
中国地质环境监测院主办
高级检索

弯曲岩溶管道溶质运移的尺度效应研究

,  ,  , 

文章导航 > 水文地质工程地质 > 2023 > 50(2): 44-53

上一篇

下一篇

赵小二, 王正一, 武桂芝, 李琪. 弯曲岩溶管道溶质运移的尺度效应研究[J]. 水文地质工程地质, 2023, 50(2): 44-53. doi: 10.16030/j.cnki.issn.1000-3665.202203050
引用本文: 赵小二, 王正一, 武桂芝, 李琪. 弯曲岩溶管道溶质运移的尺度效应研究[J]. 水文地质工程地质, 2023, 50(2): 44-53. doi: 10.16030/j.cnki.issn.1000-3665.202203050
shu
ZHAO Xiaoer, WANG Zhengyi, WU Guizhi, LI Qi. Research on the scale effects of solute transport in a bended karst conduit[J]. Hydrogeology & Engineering Geology, 2023, 50(2): 44-53. doi: 10.16030/j.cnki.issn.1000-3665.202203050
Citation: ZHAO Xiaoer, WANG Zhengyi, WU Guizhi, LI Qi. Research on the scale effects of solute transport in a bended karst conduit[J]. Hydrogeology & Engineering Geology, 2023, 50(2): 44-53. doi: 10.16030/j.cnki.issn.1000-3665.202203050
shu

弯曲岩溶管道溶质运移的尺度效应研究

  • 1.

    青岛理工大学环境与市政工程学院，山东 青岛　266033

  • 2.

    青岛佳明测控科技股份有限公司，山东 青岛　266000

  • 基金项目: 国家自然科学基金项目（42002259）
详细信息
    作者简介: 赵小二（1989-），男，博士，主要从事岩溶水文地质方面的研究。E-mail：zhaoxiaoer@qut.edu.cn

  • 中图分类号: P641.134

Research on the scale effects of solute transport in a bended karst conduit

  • 1.

    School of Environmental and Municipal Engineering, Qingdao University of Technology, Qingdao, Shandong　266033, China

  • 2.

    Jia Ming Measurement & Control, Qingdao, Shandong　266000, China

摘要

    摘要

  • 岩溶管道溶质运移的尺度效应研究对穿透曲线的正确解译非常重要，但目前针对单一弯曲管道中溶质运移尺度效应的研究仍比较缺乏。文章将岩溶管道和溶潭分别概化为透明软管和水箱，基于前期建立的水箱-管道系统（简称“管道系统”），在水箱下游设置不同长度的弯曲管道，通过示踪试验研究管道运移尺度对穿透曲线的影响，并采用暂时存储模型模拟试验曲线。结果表明：（1）随着水箱下游管道长度的增加，峰值质量浓度逐渐缓慢降低，穿透曲线上升段斜率无明显变化，穿透曲线拖尾逐渐缩短，表明运移管道长度增加对溶质运移的影响大于下游管道弯曲；（2）穿透曲线偏度系数、后段溶质羽穿透时间和溶质羽穿透时间与管道系统长度呈良好的负线性相关关系（R2>0.96）；（3）当对称和不对称水箱管道系统长度分别增加至154.5 m和164.3 m时，偏度系数接近0，穿透曲线分布接近对称；（4）弥散系数、存储区截面积和交换系数与管道系统长度呈良好的负线性相关关系，当对称和不对称水箱管道系统长度分别增加至159.9 m和178.1 m时，存储区截面积接近0，水箱导致的溶质运移滞后效应基本消失。研究结果对野外岩溶管道穿透曲线的解译具有一定指示作用。

    Research on the scale effect of solute transport in karst conduits is very important for the correct interpretation of breakthrough curves (BTCs), but the scale effect of solute transport in a bended conduit has not been examined. In this paper, a karst conduit and a pool developed within the conduit are generalized into the transparent hose and cubic pool, respectively. Based on the previously established pool-pipe system, the bended pipes with different lengths are arranged downstream of the pool, and the tracer experiments are conducted to study the effect of the transport scale on the BTCs in conduits. We use the transient storage model to simulate the experimental curves. The results show that with the increasing pipe length downstream the pool, the peak concentration gradually decreases slowly, the rising slope of the BTCs does not change significantly, and the BTC tails gradually shorten, indicating that the longer transport distance exerts a larger effect on solute transport than the conduit bend. The coefficient of skewness (CSK), breakthrough time of posterior solute plume (tre) and breakthrough time of solute plume (td) are well negatively correlated with the length of the pipe system (R2>0.96). When the length of the pipe system with the symmetrical or asymmetrical pool increases to 154.5 m and 164.3 m, respectively, the CSK is close to zero, and the BTC is nearly symmetrical. The dispersion coefficient (D), cross-sectional area of the storage zones (As) and exchange coefficient (α) have a good negative correlation with the length of the pipe system. When the length of the pipe system with the symmetrical or asymmetrical pool increases to 159.9 m and 178.1 m, respectively, the As is close to zero. Then, the solute retention caused by the pool basically disappears. The results have certain indications for the interpretation of the BTCs in field karst conduits.

    • HTML全文

  • 岩溶含水层是全球范围内重要的水资源，为超过25%的世界人口提供了饮用水[1]。岩溶管道是岩溶含水层中主要的径流通道，地表水和污染物可通过天窗、落水洞等进入岩溶管道并快速运移至四周，造成大面积地下水污染，导致岩溶含水层遭受污染[2]，因此研究岩溶管道中溶质运移过程对岩溶地下水污染物的运移预测和防治非常重要。

    定量示踪试验为岩溶地区一种常规的野外调查手段，通过示踪试验不仅可以调查地下水的连通性，还能通过定量分析和解译穿透曲线（breakthrough curve，BTC）获取岩溶管道的水力参数和溶质运移参数[3-5]。由于野外岩溶管道沿程不规则结构（溶潭、管壁粗糙度、弯曲度等）的发育，岩溶管道穿透曲线和水文地质参数具有明显的尺度效应[6]，因此尺度效应研究对穿透曲线的正确解译非常重要。很多学者已经针对均匀管道长度和不规则管道结构对尺度效应的影响开展了研究。例如，Taylor[7]在直径较小（<1 cm）、横截面均匀的直玻璃管中开展示踪试验，Hauns等[8]采用计算流体动力学（CFD）模拟研究了示踪剂在横截面均匀的直管道中的运移，均发现均匀直管道的穿透曲线拖尾程度随着在管道中运移距离（管道长度）的增加逐渐降低，穿透曲线逐渐趋近于对称分布；Zhao等[9]和Hauns等[8]通过室内示踪试验和数值示踪试验研究了溶潭、急流等结构对溶质运移的影响，发现单管道中溶潭、急流等结构的发育导致弥散和滞后效应显著增强；Hauns等[8]同时考虑管道长度和溶潭的影响，研究表明由于沿管道发育的溶潭导致的溶质运移滞后效应和在管道中运移距离增加导致的溶质运移滞后效应降低的综合结果，穿透曲线拖尾程度随着管道尺度的增加先增加后缓慢下降。虽然上述研究通过探讨下游管道长度、不规则管道结构对溶质运移的影响研究了岩溶管道溶质运移的尺度效应，但没有同时研究管道弯曲和管道长度对溶质运移的综合影响，导致两者同时存在时穿透曲线拖尾的变化规律也尚不明确。由于野外管道常常呈弯曲形态，需要进一步研究。

    Li等[10]使用长14.1 cm、内径2 cm的多孔壁圆管模拟管道，并用管道四周分布的紧密堆积的玻璃珠模拟周围基质；Faulkner等[11]采用透明有机玻璃的立方体模拟管道，管道长为57.8 cm，截面尺寸为2 cm×2 cm，在管道一侧布设充满玻璃珠的有机玻璃立方体表示基质区；Mohammadi等[12]采用长4 cm、内径2.6～10 mm的透明穿孔软塑料管表示岩溶管道，用沙子表示多孔基质；Shu等[13]采用由间距垫片隔离开的加气混凝土砌块构造室内管道和裂隙基质系统，管道长为5 m，截面尺寸为5 cm（高）×2 cm（宽）。Wang等[14]采用长10～360 cm、内径0.4 cm的硅胶管构造表征岩溶双管道结构，不考虑管道周围基质的作用。上述研究重点探讨管道和周围基质交换作用以及岩溶分支管道对溶质运移的影响机理，但是概化的室内管道长度较短，长度和管道截面的几何比尺远小于野外实际情况。

    以上研究设计了实验室尺度的物理模型开展试验，部分研究考虑了岩溶管道和周围基质的相互交换[10-13]，部分研究仅关注岩溶管道中的溶质运移情况[9, 14-15]。相比之下，以下研究概化的岩溶管道长度与管道截面的几何比尺更符合野外情况：Field等[15]将岩溶管道概化为长30.48 m、内径3.51 cm的聚乙烯管，管壁随机粘有砂石，用来表征野外岩溶管道的粗糙壁面；Zhao等[9]采用长为50 m、内径为19 mm的PVC透明圆管表征岩溶管道，采用边长为10 cm的立方体水箱表征岩溶管道中间发育的溶潭结构；分别重点讨论了岩溶分支管道导致多峰穿透曲线以及溶潭结构导致穿透曲线显著拖尾的现象和作用机理。

    我国西南岩溶区岩性以早三叠世的致密坚硬的碳酸盐岩为主，孔隙度低（石灰岩一般小于1%，白云岩一般小于5%）[16]，渗透性较低，岩溶管道同周边基质的交互作用较弱。因此，本文不考虑管道周围基质的影响，采用更符合野外实际情况的管道长度和截面尺寸进行概化，基于Zhao等[9]的岩溶管道概化方式，在实验室建立水箱-管道系统，在水箱（溶潭）下游设置不同长度的弯曲管道，研究弯曲岩溶管道中溶质运移的尺度效应。

    1.1   试验装置

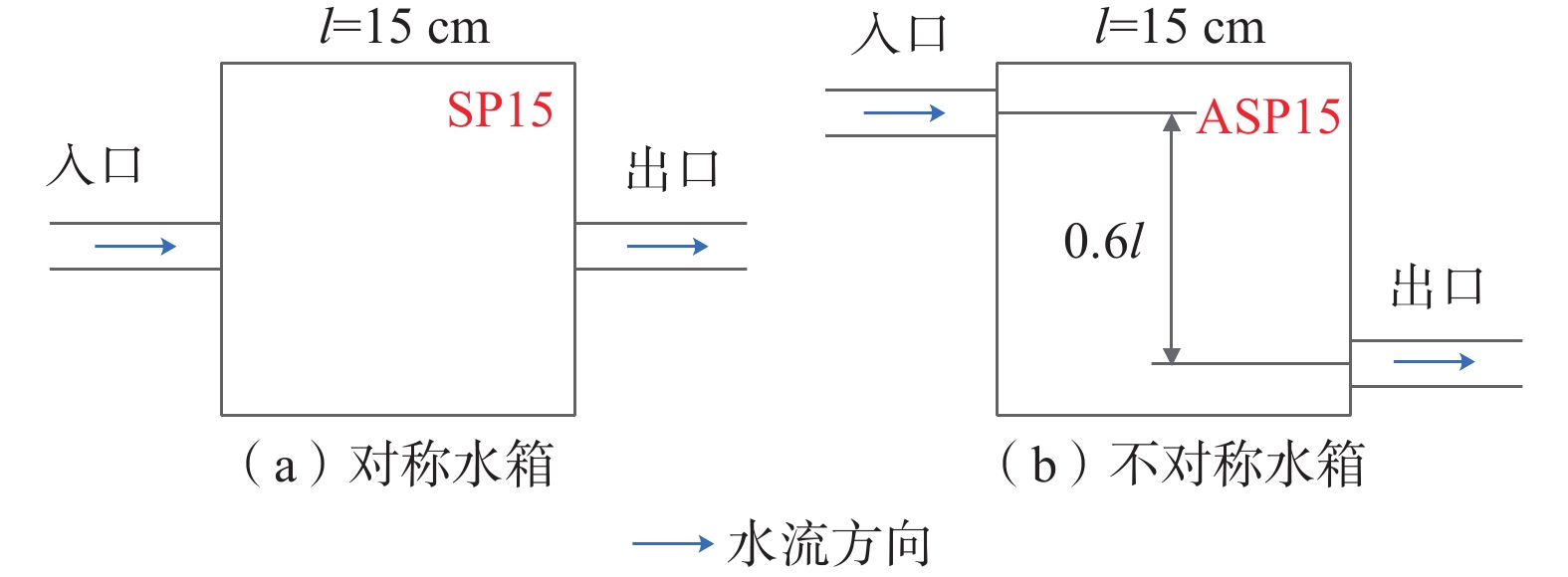
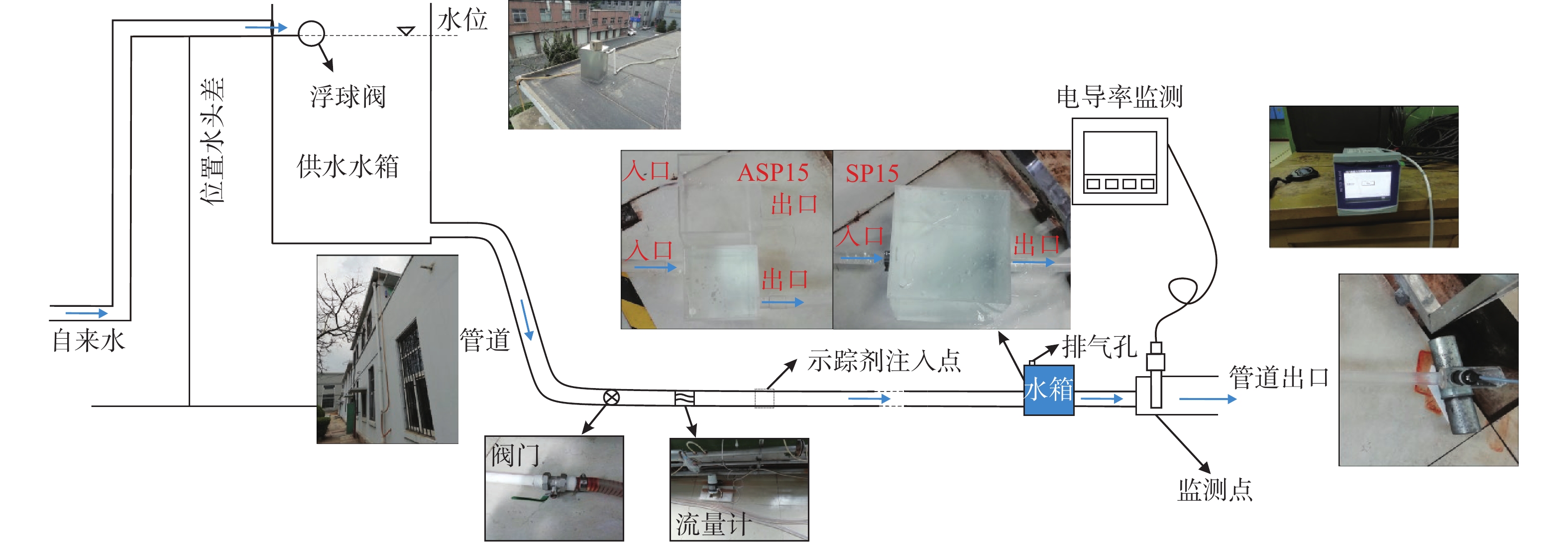
    将野外岩溶管道在室内概化为水箱-管道系统（下文简称“管道系统”），用水箱表征溶潭，用圆形截面的透明软管表征岩溶管道。本文试验装置主要由1个定水头供水水箱，1根透明软管（内径为25 mm）和2种不同形态的立方体水箱（对称水箱和不对称水箱）构成（图1）。供水水箱接收流入的水并将水排放到管道系统，同时通过浮球阀维持恒定水头；当供水水箱满时，浮球阀关闭，终止进水。为了向管道系统提供足够的流量，将供水水箱置于屋顶，供水水箱到管道出口的水头差约为7.8 m。如图2所示，对称水箱是指入口和出口位于水箱正方形面的中心位置，出入口连线平行于水箱的侧边；不对称水箱是指入口和出口位于中心线的两侧，且到水箱底部的高度相同；2种水箱的边长均为15 cm。在水箱的顶部设计排气口，注入示踪剂之前排出气泡，以保持管道和水箱中始终处于饱和水状态。通过控制阀（图1）调节管道内流量，采用电磁流量计（GFM82系列）测量流量，测量范围为0.5～21.2 m3/h，测量精度为±1.0%。为确保流量测量的稳定性，将流量计设置在控制阀下游4 m处和示踪剂注入点上游4 m处。试验装置详情可进一步查阅文献[17]。

    图 1.  试验装置示意图（修改自文献[17]）
    Figure 1.  Schematic diagram of the experimental setup （modified from Ref. [17]）
    下载: 全尺寸图片 幻灯片
    图 2.  水箱示意图
    Figure 2.  Schematic diagram of the symmetrical pool
    下载: 全尺寸图片 幻灯片

    示踪试验开始之前，调节阀门（图1）至流量稳定为0.884 m3/h，管道平均流速为0.5 m/s。设计0.5 m/s的管道流速的原因如下：①野外岩溶管道地下水流态大多为紊流，该流速对应的雷诺数约为9542，为紊流流态，符合野外情况；②预试验表明该流速条件下能监测到足够的浓度数据；③根据相似准则，该室内管道流速对应的野外岩溶管道流速符合实际情况（见1.3节）。如果忽略水在管道中流动的水头损失，根据供水水箱到管道出口的7.8 m水头差计算得到的管道出口流速将远大于设计流速；但在实际情况下，存在水流黏滞力导致的与管道长度成正比的沿程水头损失以及水流经过阀门和立方体水箱引起的局部水头损失，尤其是调节阀门开度较小时，会导致较大的水头损失，使得最终管道流速为0.5 m/s。

    1.2   示踪试验

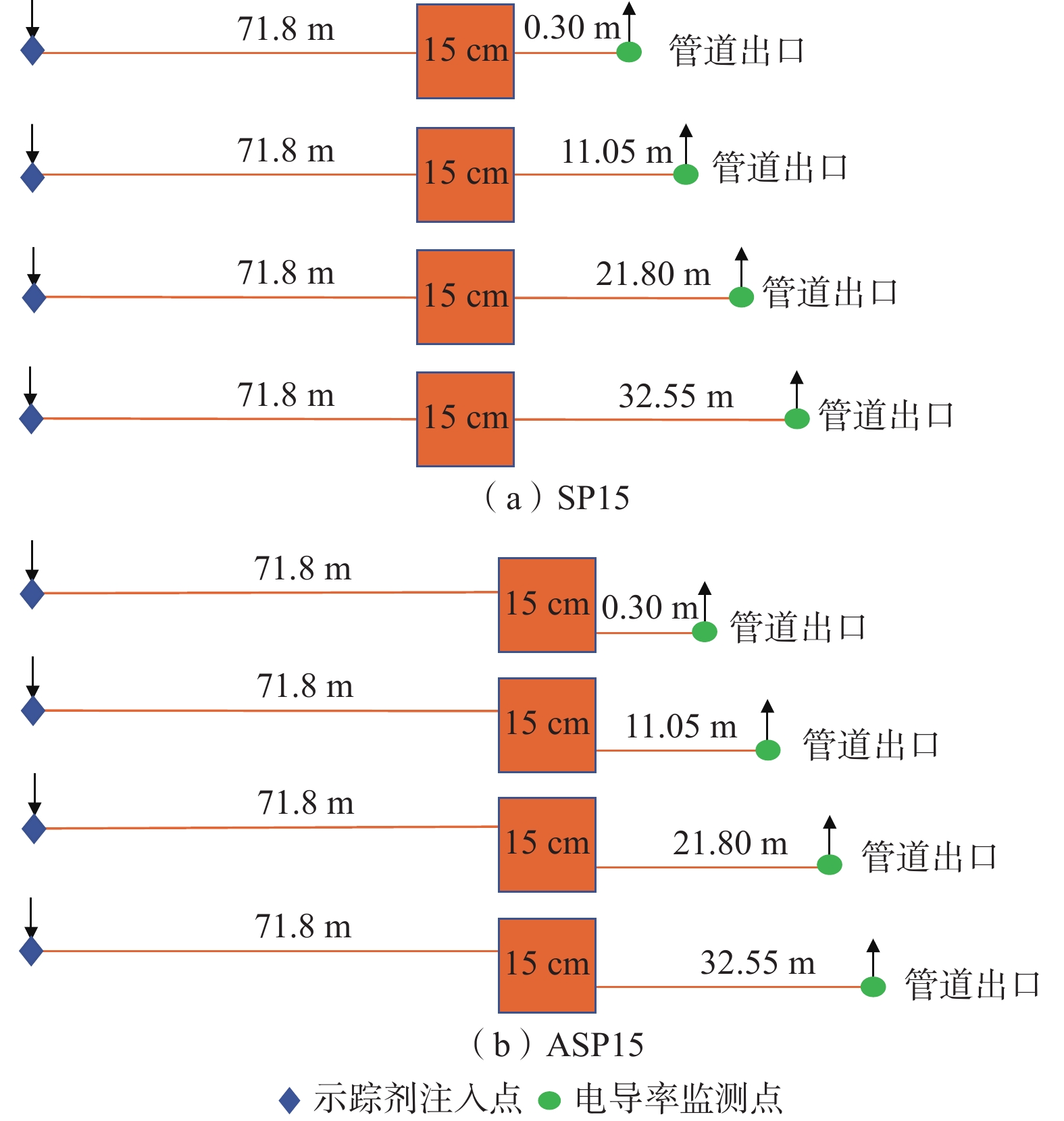
    为了研究岩溶管道溶质运移的尺度效应，分别在管道系统中添加一个对称水箱（SP15）和一个不对称水箱（ASP15）（图1、图2），设计示踪剂注入点到立方体水箱的距离为71.8 m，水箱到管道系统出口的长度分别为0.30，11.05，21.80，32.55 m（图3），则管道系统长度L（从示踪剂注入点到管道出口处的长度）依次为72.25，83.00，93.75，104.50 m。为了表征野外弯曲岩溶管道，设计管道呈弯曲形式摆放（图4）。

    图 3.  不同管道长度的水箱管道系统示意图
    Figure 3.  Schematic diagram of the pool-pipe system with different lengths
    下载: 全尺寸图片 幻灯片
    图 4.  不同长度管道的摆放位置示意图（俯视图）
    Figure 4.  Schematic diagram of the pipe placement with different lengths （top view）
    下载: 全尺寸图片 幻灯片

    本试验示踪剂为质量浓度100 g/L的NaCl溶液，每次试验采用注射器将5 mL（即0.5 g）的示踪剂快速注入到管道中。由于注入时间较短，为1 s左右，可视为瞬时注入。示踪剂注入同时，采用M300 Water电导率仪测量管道出口处的电导率值，电导率监测时间间隔为1 s，并通过质量浓度-电导率曲线校正得到示踪质量浓度值。每个试验重复3次，确保试验结果的准确性。

    1.3   室内模型设计相似准则

    为了让实验室尺度的物理模型能表征野外尺度的岩溶系统，需要满足几何和动力相似准则[18-19]。几何相似是指野外尺度的岩溶系统和实验室尺度的物理模型的几何形状相似，即对应的线段长度成比例，且不同线段的长度比尺（λ）固定不变。由于圆形或椭圆形横截面在潜水洞穴通道中很常见[1]，因此选择圆形截面管道来近似代表岩溶管道，该概化方式已经被用于岩溶管道溶质运移的研究[9, 14-15]；其长度比尺为λ=Lr/L，L和Lr分别为实验室管道系统和野外岩溶管道的长度。本文设计室内管道长度分别为72.25，83.00，93.75，104.50 m，对于1000 m长度的岩溶管道[8, 20]，计算得到λ为1个数量级左右。溶潭的体积等于立方体水箱的体积乘上λ3，计算结果符合实际情况[8]。对于充满水的有压管流，当室内管道流和野外岩溶管道流的雷诺数相等时，则满足动力相似。假设野外和室内水流的运动粘度保持不变，则野外岩溶管道流速为v/λ，其中v为实验室管道的平均流速。如果λ为1个数量级，则室内0.5 m/s的平均流速所对应的野外流速符合实际情况[1, 21]。本文重点研究溶质在溶潭下游弯曲岩溶管道中运移的尺度效应，在设计实验室尺度的物理模型时，忽略真实岩溶管道的粗糙度是合理的[22-23]，因为它们不能产生显著的BTC拖尾。虽然简化的管道系统与内部结构复杂（包括粗糙度、管道截面的沿程变化等）的真实岩溶管道相比要简单得多，不能完全满足相似性，但通过该试验研究弯曲管道和管道长度对溶质运移的影响，能一定程度上反映弯曲岩溶管道溶质运移的尺度效应。

    1.4   穿透曲线分析方法

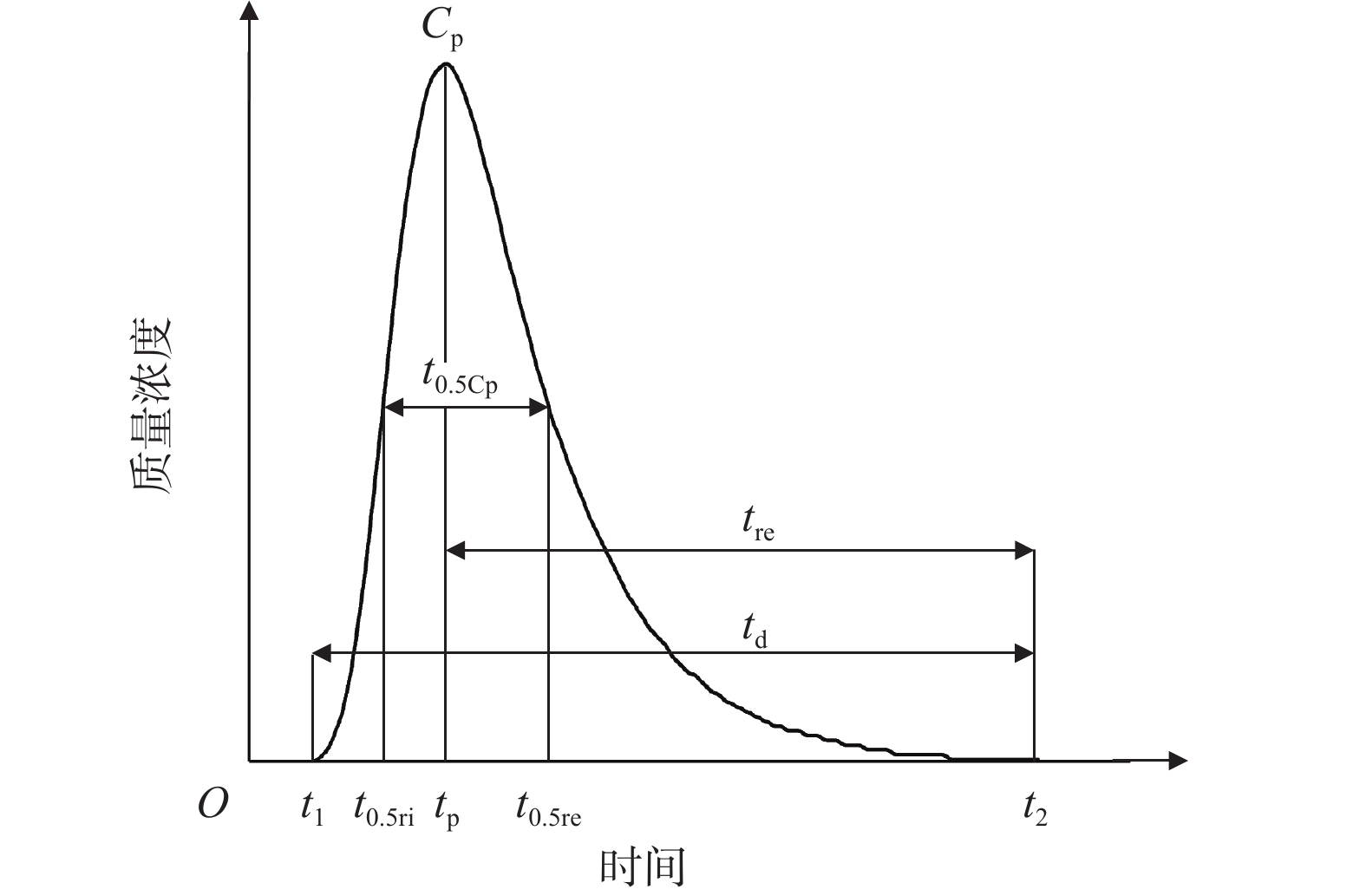
    穿透曲线通常由三部分组成：上升段、峰值浓度和下降段，相应的特征参数见图5和表1。本文通过分析穿透曲线得到8个特征参数，分别为回收率（Rt）、平均运移时间（tm）、平均示踪流速（v）、时间方差（σt2）、偏度系数（CSK）[24]、后段溶质羽穿透时间（tre）[24]、主体溶质羽穿透时间（t0.5Cp）[12]、溶质羽穿透时间（td）[2]。

    图 5.  典型的穿透曲线及特征参数
    注：Cp为峰值质量浓度；t1为示踪剂最先到达时刻；tp为峰值质量浓度到达时刻；t2为示踪剂最后检出时刻；t0.5ri为浓度上升至一半时峰值质量浓度所对应的时刻；t0.5re为浓度下降至一半时峰值质量浓度所对应的时刻。
    Figure 5.  Typical breakthrough curve and its characteristic parameters
    下载: 全尺寸图片 幻灯片
    表 1.  穿透曲线特征参数
    Table 1.  Characteristic parameters of breakthrough curve
    特征参数参数分类计算方法
    Cp最大示踪剂浓度
    Rt示踪剂回收率
    tm水力参数
    v水力参数
    σt2水力参数
    CSK水力参数
    tre水力参数
    t0.5Cp水力参数
    td水力参数
    注：C（t）为在任意t时刻的质量浓度；Q（t）为t时刻的流量；M为示踪剂注入质量。
     | Show Table
    DownLoad: CSV

    采用Qtracer2软件对穿透曲线进行定量分析，可获得最大示踪剂浓度、示踪剂回收率和管道水力参数[22, 25]。CSK、tre、t0.5Cp、td这4个参数可由表1的计算公式算出，其他参数则由Qtracer2软件计算得出。

    1.5   模拟方法

    本文采用暂时存储模型（TSM）模拟试验结果，该模型把模拟区划分为主通道和存储区[26]，两区之间存在线性质量交换，即两区间的溶质交换量与浓度差呈正比。在主通道中，溶质通过对流弥散向下游运移，例如管道部分。存储区中忽略下游运移，无对流弥散过程；水箱内涡流流速相比主管道中心的快速流较慢，导致溶质流经水箱时暂时性滞留其中，可视为存储区[27]。采用OTIS软件[27]求解TSM。示踪剂为NaCl溶液，不考虑化学反应，模型方程为式（3）（4）：

    ∂C∂t=−QA∂C∂x+1A∂∂x(AD∂C∂x)+α(Cs−C) (3)
    dCsdt=αAAs(C−Cs) (4)

    式中：t——时间/s；

    x——注入点下游距离/m；

    C、Cs——主通道和存储区中溶质质量浓度/（mg·L−1）；

    A、As——主通道和存储区的截面积/m2；

    Q——体积流量/（m3·s−1）；

    D——弥散系数/（m2·s−1）；

    α——交换系数/s−1。

    采用Damköhler 提出的无量纲量（DaI）表明参数识别的可靠性[28]：

    DaI=α(1+AAs)Lu (5)

    式中：u——平均对流速度/（m∙s−1），u=Q/A。

    DaI反映了平均对流运移时间与暂时储存区相互作用时间尺度的比值。当DaI值为0.1～1.0时，参数的不确定性很小[28]。对于本文瞬时注入示踪剂的情况，DaI值变化范围为0.6～60.0时说明参数的不确定性有限[29]，进而表明参数的合理性[30]。

    2.1   试验结果与分析

    表2为不同管道系统长度（L）的穿透曲线特征参数。如表2所示，回收率基本大于90%，仅1组试验回收率略小于90%，表明试验结果的合理性。如图6所示，随着水箱下游管道长度的增加，峰值出现时间和示踪剂浓度出现时间逐渐滞后，穿透曲线峰值浓度逐渐降低，原因是流量不变，因而溶质在管道系统中的运移时间增加，即弥散作用时间增加，导致溶质羽的分布更加分散。随着水箱下游管道长度的增加，穿透曲线上升至峰值浓度的速率基本不变，曲线拖尾逐渐缩短。

    表 2.  不同管道系统长度的穿透曲线特征参数
    Table 2.  Characteristic parameters of breakthrough curve of the pipe system with different lengths
    水箱结构L/mv/（m·s−1）tm/minσt2/min2CSKtre/st0.5Cp/std/sRt/%
    SP1572.250.4472.70040.157680.14721751218791.97
    83.000.4503.07450.153200.12741641217891.92
    93.750.4583.41240.140150.10971481316192.50
    104.500.4673.73170.109960.08891251313789.27
    ASP1572.250.4462.70160.0523050.0847892010594.99
    83.000.4523.05940.0487100.072282219896.88
    93.750.4573.42270.0450400.062074219091.83
    104.500.4613.77390.0440960.055763217992.36
     | Show Table
    DownLoad: CSV
    图 6.  水箱下游管道长度对穿透曲线的影响（图中为管道系统长度）
    Figure 6.  Influence of the pipe length downstream of the pool on the breakthrough curve (the length of the pool-pipe system is shown in the figure)
    下载: 全尺寸图片 幻灯片

    图7表明了主要穿透曲线特征参数与L的关系。2种水箱-管道系统的v均随着L略微增加，可近似认为保持不变，这是由于管道系统的流量保持不变。tm与L呈良好的正线性相关关系（R2>0.998），并且2种水箱的tm基本相等。

    图 7.  穿透曲线特征参数与L的关系
    Figure 7.  Relationships between the characteristic parameters of the BTCs and L
    下载: 全尺寸图片 幻灯片

    2种水箱的CSK、tre和td都与L呈良好的负线性相关关系（R2>0.96），表明穿透曲线拖尾程度逐渐降低，穿透曲线渐渐趋近于对称。假设CSK=0时，对称和不对称水箱计算的L分别为154.5 m和164.3 m，表明当示踪剂流出水箱后在下游管道中分别运移82.55 m和92.35 m时，穿透曲线的形态接近对称正态分布。t0.5Cp基本不变，平均示踪流速基本一致，说明包含大于一半最大浓度溶液的管道长度基本不变，进而说明溶质羽的空间分布在水箱下游单管道中随着运移尺度的增加近似保持不变，这是由于溶质羽在单管道中的混合弥散作用较弱导致的。

    对称水箱的CSK、tre、td远大于不对称水箱，这是由于对称水箱的穿透曲线拖尾程度比不对称水箱严重，而对称水箱的t0.5Cp小于不对称水箱，可能是由于溶质羽在不对称水箱内的混合更加剧烈导致的。

    2.2   模拟结果与分析

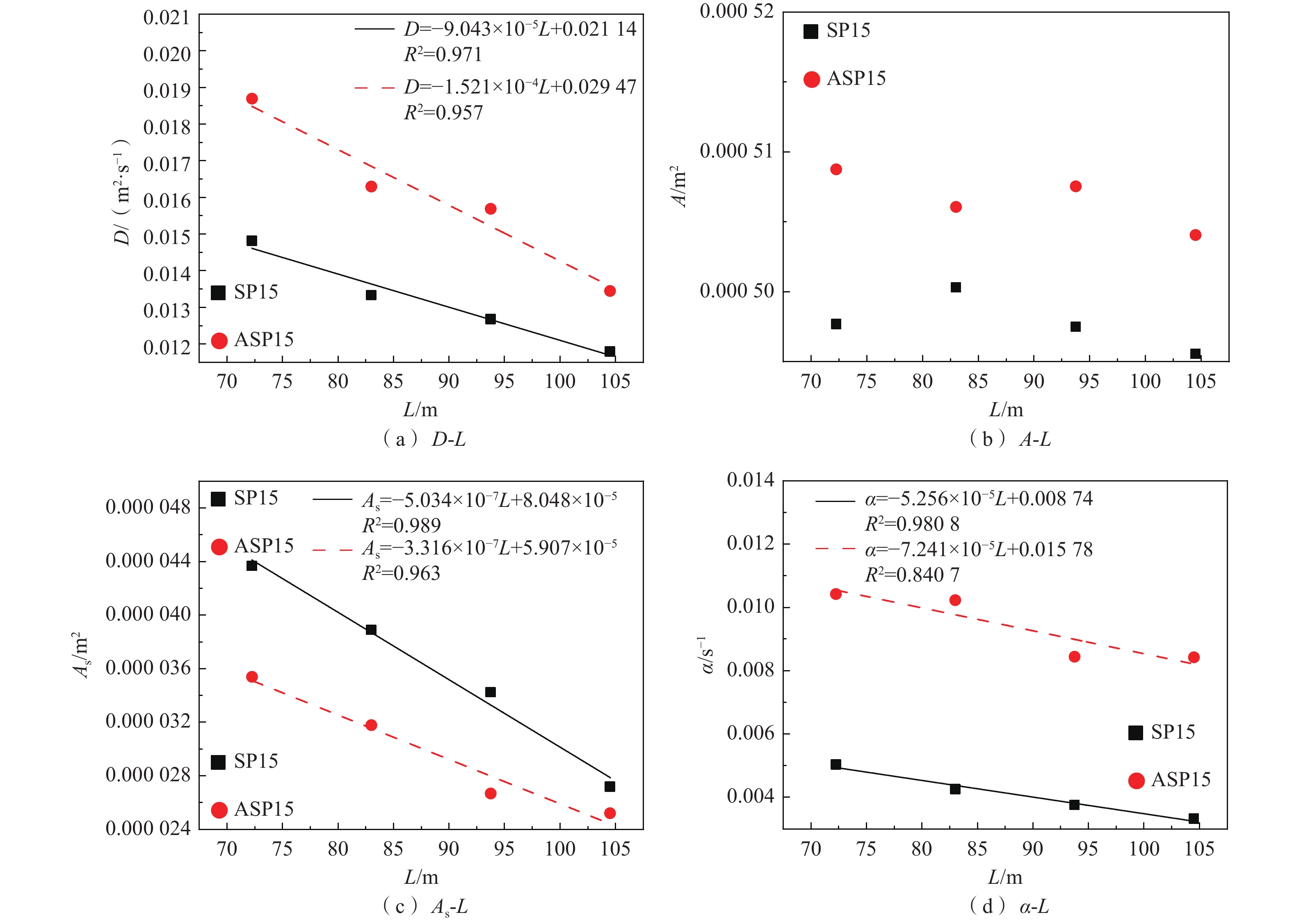
    不同管道长度下，2种水箱的模型参数见表3。瞬时注入条件下DaI值位于0.6～60.0时，参数比较合理[30]；对称和不对称水箱-管道系统的DaI变化范围分别为12.4～13.5和34.7～38.0，说明本文模型参数的合理性。如图8所示，2种水箱的弥散系数（D）、存储区截面积（As）及交换系数（α ）都随着水箱下游管道长度的增加而减小，且与管道系统长度呈良好的线性关系（R2>0.96，不对称水箱α 的R2为0.84）。随着水箱下游管道长度的增加，水箱所占据整个管道系统的比例逐渐下降，从而水箱导致的溶质弥散和两区溶质交换的平均效应逐渐降低，由于D和α 表示整个管道系统的平均值，因此两者均逐渐减小。随着水箱下游管道长度的增加，对称水箱存储区容积（Vs=As×L）的变化范围为0.0028～0.0032 m3，不对称水箱存储区容积的变化范围为0.0025～0.0026 m3，变化较小。前期研究表明[9]，存储区容积大小取决于水箱容积的大小，试验管道系统中水箱容积不变，因此存储区容积大小随着下游管道长度基本不变（表3）；管道系统长度逐渐增加，导致As（As=Vs/L）下降，进而导致溶质在水箱中的暂时存储效应逐渐减弱。假设As=0，则对称和不对称水箱的计算L分别为159.9 m和178.1 m，与上节中假设偏度系数为0时计算的L（分别为154.5 m和164.3 m）接近，表明当示踪剂流出水箱后在下游管道中分别运移87.95 m和106.15 m时，上游水箱导致的溶质运移滞后效应基本消失，溶质运移过程接近对流弥散过程，穿透曲线的形态接近对称正态分布。

    表 3.  不同管道系统长度的模型参数
    Table 3.  Model parameters of the pipe system with different lengths
    水箱结构L/mD/（m2·s−1）A/m2As/m2α/s−1Vs/m3DaI
    SP1572.251.48×10−24.98×10−44.37×10−55.04×10−33.16×10−313.2
    83.001.33×10−25.00×10−43.89×10−54.26×10−33.23×10−312.6
    93.751.27×10−24.97×10−43.42×10−53.76×10−33.21×10−312.4
    104.501.18×10−24.96×10−42.72×10−53.32×10−32.84×10−313.5
    ASP1572.251.87×10−25.09×10−43.54×10−51.04×10−22.56×10−334.7
    83.001.63×10−25.06×10−43.18×10−51.02×10−22.64×10−337.3
    93.751.57×10−25.08×10−42.67×10−58.44×10−22.50×10−336.5
    104.501.34×10−25.04×10−42.52×10−58.42×10−22.63×10−338.0
     | Show Table
    DownLoad: CSV
    图 8.  模型参数与L的关系
    Figure 8.  Relationships between the model parameters and L
    下载: 全尺寸图片 幻灯片

    对称水箱和不对称水箱主通道截面积（A）的变化范围分别为4.96×10−4～5.00×10−4 m2和5.04×10−4～5.09×10−4 m2，参数变化范围很小，可视作基本不变。实际管道截面积和水箱尺寸是影响A的主要因素，随着管道系统长度的增加，这两个因素保持不变，因而A基本不变。

    根据穿透曲线偏度系数（CSK）与管道系统长度（L）的关系式（CSK=−0.00179L+0.27664，SP15；CSK=−0.000904L+0.14856，ASP15）计算得到：L分别达到154.5 m和164.3 m时，穿透曲线接近对称；根据暂时存储区截面积（As）与管道系统长度（L）的关系式（As=−5.034×10−7L+8.048×10−5，SP15；As=−3.316×10−7L+5.907×10−5，ASP15）计算得到：L分别为159.9 m和178.1 m时，溶质运移滞后效应逐渐消失。管道弯曲可能导致溶质暂时性存储现象[18, 31]，直管道中穿透曲线拖尾程度随着运移距离的增加逐渐减弱，本文随着水箱下游弯曲管道尺度的增加，穿透曲线拖尾逐渐消失，该结论和直管道中穿透曲线的变化规律基本一致，表明管道弯曲对溶质运移滞后的影响小于运移距离增加对溶质运移的影响。

    实际情况下岩溶管道结构复杂多样，试验装置中管道和水箱不能完全反应野外情况，本文溶质运移的尺度效应在野外难以全部适用，尤其是溶质运移路径较长时，由于沿程发育的管道结构未知，穿透曲线拖尾程度随着溶质运移尺度增加的变化规律难以确定，赵良杰等[6]指出两区模型参数随管道运移尺度的增加没有明确的变化规律。在野外岩溶管道中，随着下游管道尺度的增加，可能会伴随暂时存储区结构（溶潭等）的发育，暂时存储区导致的溶质运移滞后效应增强和运移距离增加导致的滞后效应减弱同时存在时，穿透曲线拖尾程度和模型参数的变化规律难以确定。

    尽管如此，上述结论对野外岩溶管道穿透曲线的解译仍有指示作用：在较长的岩溶管道出口监测的穿透曲线不具有明显拖尾时，并不能说明沿程一定没有溶潭的发育。当溶潭发育在上游，下游管道较长且发育的不规则结构（弯曲度、粗糙管壁等）不能导致显著的暂时性存储时，上游溶潭导致的穿透曲线拖尾现象经过下游较长距离的运移时可能逐渐消失，管道出口的穿透曲线则不会呈现显著的拖尾现象。这和Hauns等[8]在野外岩溶管道中开展示踪试验的研究结果基本一致：由于溶潭的发育，注入点下游35 m的穿透曲线呈现严重的拖尾现象，但注入点下游873 m的穿透曲线接近对称。该情况下，为了进一步识别初始示踪剂注入点到初始监测点这一段管道是否发育溶潭结构，需要在示踪剂注入点下游不同位置补充监测穿透曲线。当某个点的穿透曲线呈现严重拖尾时，表明该点上游发育溶潭结构，而该点下游到初始监测点这一段则较大可能不发育溶潭结构。

    示踪剂注入点到穿透曲线监测点路径较长时，穿透曲线是沿程不同管道结构（溶潭、粗糙度、弯曲度、管道长度等）的综合效应，因而仅由监测点的穿透曲线形态反演上游岩溶管道结构时存在不确定性和多解性。当穿透曲线呈现单峰且拖尾较严重时[9]，即曲线下降段存在一个浓度梯度下降[32]时，说明岩溶管道中发育溶潭结构，同时溶潭发育也导致钝峰的出现[33]，这也可作为溶潭发育的证据。而穿透曲线拖尾不明显时，则存在多种可能性，可能是无溶潭结构的发育，也可能是监测点上游较远处存在溶潭结构，管道下游无较明显的暂时存储区结构发育，导致穿透曲线拖尾随着运移尺度增加逐渐降低直至监测点拖尾基本消失[8]，这种情况下在示踪剂注入点下游布设多个穿透曲线监测点对于识别岩溶管道结构非常有必要。除此之外，溶质运移路径较长时，可能导致示踪剂滞留于管道结构中未及时排出，进而导致示踪剂回收率较低[33-34]。谢国文等[34]指出，不能根据取样点未接收到示踪剂信号而排除取样点和示踪投放点的水力联系，示踪剂投放点（上湾落水洞）到取样点（隧道涌水点）的流经路径较长（1950 m）也可能导致示踪剂滞留于地下管道中而不能到达取样点；其他证据表明隧道涌水点和上湾落水洞之间存在水力联系。

    （1）随着水箱下游弯曲管道长度的增加，峰值浓度逐渐缓慢降低，穿透曲线上升段斜率无明显变化，穿透曲线拖尾逐渐缩短。

    （2）2种水箱的偏度系数、后段溶质羽穿透时间和溶质羽穿透时间与管道系统长度呈良好的负线性相关关系（R2>0.96）。当对称和不对称水箱管道系统长度分别增加至154.5 m和164.3 m时，穿透曲线的偏度系数接近0，穿透曲线分布接近对称。2种水箱的弥散系数、存储区截面积和交换系数都与管道系统长度呈良好的负线性相关关系，当对称和不对称水箱管道系统长度分别增加至159.9 m和178.1 m时，存储区截面积接近0，水箱导致的溶质运移滞后效应基本消失。2种水箱的主通道截面积随着水箱下游管道长度基本不变。

    （3）本文结论对野外岩溶管道穿透曲线的解译有一定指示作用：在较长的岩溶管道出口监测的穿透曲线不具有明显拖尾时，并不能说明沿程一定没有溶潭的发育，为了进一步识别是否发育溶潭结构，需要在示踪剂注入点下游不同位置补充监测穿透曲线。示踪剂注入点到穿透曲线监测点路径较长时，监测点穿透曲线是沿程不同管道结构（溶潭、粗糙度、弯曲度、管道长度等）的综合效应，因而仅由监测点的穿透曲线形态反演上游岩溶管道结构时存在不确定性和多解性，这种情况下在示踪剂注入点下游布设多个穿透曲线监测点对于识别岩溶管道结构非常有必要。

  • 图 1  试验装置示意图（修改自文献[17]）

    Figure 1. 

    下载: 全尺寸图片 幻灯片

    图 2  水箱示意图

    Figure 2. 

    下载: 全尺寸图片 幻灯片

    图 3  不同管道长度的水箱管道系统示意图

    Figure 3. 

    下载: 全尺寸图片 幻灯片

    图 4  不同长度管道的摆放位置示意图（俯视图）

    Figure 4. 

    下载: 全尺寸图片 幻灯片

    图 5  典型的穿透曲线及特征参数

    Figure 5. 

    下载: 全尺寸图片 幻灯片

    图 6  水箱下游管道长度对穿透曲线的影响（图中为管道系统长度）

    Figure 6. 

    下载: 全尺寸图片 幻灯片

    图 7  穿透曲线特征参数与L的关系

    Figure 7. 

    下载: 全尺寸图片 幻灯片

    图 8  模型参数与L的关系

    Figure 8. 

    下载: 全尺寸图片 幻灯片

    表 1  穿透曲线特征参数

    Table 1.  Characteristic parameters of breakthrough curve

    特征参数参数分类计算方法
    Cp最大示踪剂浓度
    Rt示踪剂回收率
    tm水力参数
    v水力参数
    σt2水力参数
    CSK水力参数
    tre水力参数
    t0.5Cp水力参数
    td水力参数
    注：C（t）为在任意t时刻的质量浓度；Q（t）为t时刻的流量；M为示踪剂注入质量。
    下载: 导出CSV

    表 2  不同管道系统长度的穿透曲线特征参数

    Table 2.  Characteristic parameters of breakthrough curve of the pipe system with different lengths

    水箱结构L/mv/（m·s−1）tm/minσt2/min2CSKtre/st0.5Cp/std/sRt/%
    SP1572.250.4472.70040.157680.14721751218791.97
    83.000.4503.07450.153200.12741641217891.92
    93.750.4583.41240.140150.10971481316192.50
    104.500.4673.73170.109960.08891251313789.27
    ASP1572.250.4462.70160.0523050.0847892010594.99
    83.000.4523.05940.0487100.072282219896.88
    93.750.4573.42270.0450400.062074219091.83
    104.500.4613.77390.0440960.055763217992.36
    下载: 导出CSV

    表 3  不同管道系统长度的模型参数

    Table 3.  Model parameters of the pipe system with different lengths

    水箱结构L/mD/（m2·s−1）A/m2As/m2α/s−1Vs/m3DaI
    SP1572.251.48×10−24.98×10−44.37×10−55.04×10−33.16×10−313.2
    83.001.33×10−25.00×10−43.89×10−54.26×10−33.23×10−312.6
    93.751.27×10−24.97×10−43.42×10−53.76×10−33.21×10−312.4
    104.501.18×10−24.96×10−42.72×10−53.32×10−32.84×10−313.5
    ASP1572.251.87×10−25.09×10−43.54×10−51.04×10−22.56×10−334.7
    83.001.63×10−25.06×10−43.18×10−51.02×10−22.64×10−337.3
    93.751.57×10−25.08×10−42.67×10−58.44×10−22.50×10−336.5
    104.501.34×10−25.04×10−42.52×10−58.42×10−22.63×10−338.0
    下载: 导出CSV
    • 参考文献(34)
  • [1]

    FORD D C, WILLIAMS P W. Karst hydrogeology and geomorphology[M]. West Sussex, England: John Wiley & Sons Ltd, 2007.

    [2]

    MORALES T,VALDERRAMA I F D,JESÚS A U,et al. Predicting travel times and transport characterization in karst conduits by analyzing tracer-breakthrough curves[J]. Journal of Hydrology,2007,334(1/2):183 − 198.

    [3]

    GOLDSCHEIDER N,MEIMAN J,PRONK M,et al. Tracer tests in karst hydrogeology and speleology[J]. International Journal of speleology,2008,37(1):27 − 40. doi: 10.5038/1827-806X.37.1.3

    [4]

    杨平恒,袁道先,蓝家程,等. 基于在线高分辨率监测和定量计算的岩溶地下水示踪试验[J]. 西南大学学报(自然科学版),2013,35(2):103 − 108. [YANG Pingheng,YUAN Daoxian,LAN Jiacheng,et al. Tracing test of a karst aquifer based on online,high-resolution monitoring and quantitative calculation[J]. Journal of Southwest University (Natural Science Edition),2013,35(2):103 − 108. (in Chinese with English abstract)

    [5]

    程亚平,陈余道. 岩溶地下河定量示踪研究方法综述[J]. 桂林理工大学学报,2016,36(2):242 − 246. [CHENG Yaping,CHEN Yudao. Review of quantitative tracing studies on karst underground river[J]. Journal of Guilin University of Technology,2016,36(2):242 − 246. (in Chinese with English abstract)

    [6]

    赵良杰,杨杨,易连兴,等. 应用物理非平衡CDE模型反演岩溶管道流参数[J]. 工程勘察,2014,42(9):56 − 59. [ZHAO Liangjie,YANG Yang,YI Lianxing,et al. Application of physical nonequilibrium CDE model to inverse hydrogeological parameters of karst conduit[J]. Geotechnical Investigation & Surveying,2014,42(9):56 − 59. (in Chinese with English abstract)

    [7]

    TAYLOR G. The dispersion of matter in turbulent flow through a pipe[J]. Proceedings of the Royal Society of London,1954,223:446 − 468.

    [8]

    HAUNS M,JEANNIN P Y,ATTEIA O. Dispersion,retardation and scale effect in tracer breakthrough curves in karst conduits[J]. Journal of Hydrology,2001,241(3):177 − 193.

    [9]

    ZHAO Xiaoer,CHANG Yong,WU Jichun,et al. Laboratory investigation and simulation of breakthrough curves in karst conduits with pools[J]. Hydrogeology Journal,2017,25(8):2235 − 2250. doi: 10.1007/s10040-017-1626-9

    [10]

    LI Guangquan,LOPER D E,KUNG R. Contaminant sequestration in karstic aquifers:Experiments and quantification[J]. Water Resources Research,2008,44(2):401 − 422.

    [11]

    FAULKNER J,HU B X,KISH S,et al. Laboratory analog and numerical study of groundwater flow and solute transport in a karst aquifer with conduit and matrix domains[J]. Journal of Contaminant Hydrology,2009,110(1/2):34 − 44.

    [12]

    MOHAMMADI Z,GHARAAT M J,FIELD M. The effect of hydraulic gradient and pattern of conduit systems on tracing tests:Bench-scale modeling[J]. Ground Water,2018,57(1):110 − 125.

    [13]

    SHU Longcang,ZOU Zhike,LI Fulin,et al. Laboratory and numerical simulations of spatio-temporal variability of water exchange between the fissures and conduits in a karstic aquifer[J]. Journal of Hydrology,2020,590(11):125219.

    [14]

    WANG Chaoqi,WANG Xiaoguang,MAJDALANI S,et al. Influence of dual conduit structure on solute transport in karst tracer tests:An experimental laboratory study[J]. Journal of Hydrology,2020,590:125255. doi: 10.1016/j.jhydrol.2020.125255

    [15]

    FIELD M S,LEIJ F J. Solute transport in solution conduits exhibiting multi-peaked breakthrough curves[J]. Journal of Hydrology,2012,440/441:26 − 35. doi: 10.1016/j.jhydrol.2012.03.018

    [16]

    袁道先. 中国西南部的岩溶及其与华北岩溶的对比[J]. 第四纪研究,1992,12(4):352 − 361. [YUAN Daoxian. Karst in Southwest China and its comparison with karst in North China[J]. Quaternary Sciences,1992,12(4):352 − 361. (in Chinese with English abstract)

    [17]

    ZHAO Xiaoer,CHANG Yong,WU Jichun,et al. Investigating the relationships between parameters in the transient storage model and the pool volume in karst conduits through tracer experiments[J]. Journal of Hydrology,2021,593:125825. doi: 10.1016/j.jhydrol.2020.125825

    [18]

    WU Yuexia,HUNKELER D. Hyporheic exchange in a karst conduit and sediment system – A laboratory analog study[J]. Journal of Hydrology,2013,501:125 − 132. doi: 10.1016/j.jhydrol.2013.07.040

    [19]

    MOHAMMADI Z,ILLMAN W A,FIELD M. Review of laboratory scale models of karst aquifers:Approaches,similitude,and requirements[J]. Ground Water,2021,59(2):163 − 174. doi: 10.1111/gwat.13052

    [20]

    郭芳,陈坤琨,姜光辉. 岩溶地下河沉积物对氨氮的等温吸附特征[J]. 环境科学,2011,32(2):501 − 507. [GUO Fang,CHEN Kunkun,JIANG Guanghui. Characteristic of ammonia nitrogen adsorption on karst underground river sediments[J]. Environmental Science,2011,32(2):501 − 507. (in Chinese with English abstract)

    [21]

    BARBERA J A,MUDARRA M,ANDREO B,et al. Regional-scale analysis of karst underground flow deduced from tracing experiments:Examples from carbonate aquifers in Malaga Province,Southern Spain[J]. Hydrogeology Journal,2018,26(1):23 − 40. doi: 10.1007/s10040-017-1638-5

    [22]

    FIELD M. The QTRACER2 program for tracer-breakthrough curve analysis for tracer tests in karstic aquifers and other hydrologic systems[M]. Washington: US Environmental Protection Agency, 2002.

    [23]

    ZHANG Qing,LUO Shaohe,MA Haichun,et al. Simulation on the water flow affected by the shape and density of roughness elements in a single rough fracture[J]. Journal of Hydrology,2019,573:456 − 468. doi: 10.1016/j.jhydrol.2019.03.069

    [24]

    SCHMADEL N M,WARD A S,KURZ M J,et al. Stream solute tracer timescales changing with discharge and reach length confound process interpretation[J]. Water Resources Research,2016,52(4):3227 − 3245. doi: 10.1002/2015WR018062

    [25]

    陈余道,程亚平,王恒,等. 岩溶地下河管道流和管道结构及参数的定量示踪—以桂林寨底地下河为例[J]. 水文地质工程地质,2013,40(5):11 − 15. [CHEN Yudao,CHENG Yaping,WANG Heng,et al. Quantitative tracing study of hydraulic and geometric parameters of a karst underground river:Exemplified by the Zhaidi Underground River in Gulin[J]. Hydrogeology & Engeneering Geology,2013,40(5):11 − 15. (in Chinese with English abstract)

    [26]

    BENCALA,K E,WALTERS R A. Simulation of solute transport in a mountain pool-and-riffle stream a transient storage model[J]. Water Resources Research,1983,19(3):718 − 724. doi: 10.1029/WR019i003p00718

    [27]

    RUNKEL R L. One-dimensional transport with inflow and storage （OTIS）: A solute transport model for streams and rivers[R]. Reston: US Geological Survey, 1998.

    [28]

    WAGNER B J,HARVEY J W. Experimental design for estimating parameters of rate-limited mass transfer:Analysis of stream tracer studies[J]. Water Resources Research,1997,33(7):1731 − 1741. doi: 10.1029/97WR01067

    [29]

    SCHMID B H. Simplification in longitudinal transport modeling:Case of instantaneous slug releases[J]. Journal of Hydrologic Engineering,2004,9(4):319 − 324. doi: 10.1061/(ASCE)1084-0699(2004)9:4(319)

    [30]

    SCHMID,B H,INNOCENTI I,SANFILIPPO U. Characterizing solute transport with transient storage across a range of flow rates:The evidence of repeated tracer experiments in Austrian and Italian streams[J]. Advances in Water Resources,2010,33(11):1340 − 1346. doi: 10.1016/j.advwatres.2010.06.001

    [31]

    GOLDSCHEIDER N. A new quantitative interpretation of the long-tail and plateau-like breakthrough curves from tracer tests in the artesian karst aquifer of Stuttgart,Germany[J]. Hydrogeology Journal,2008,16(7):1311 − 1317. doi: 10.1007/s10040-008-0307-0

    [32]

    陈亚洲,董维红. 利用示踪试验时间-浓度曲线分析岩溶管道结构特征[J]. 水文地质工程地质,2022,49(1):41 − 47. [CHEN Yazhou,DONG Weihong. Analysis of structural characteristics of karst conduit by time-concentration curve of tracer test[J]. Hydrogeology & Engineering Geology,2022,49(1):41 − 47. (in Chinese with English abstract)

    [33]

    赵一,李衍青,覃星铭,等. 南洞地下河岩溶管道展布及结构特征的示踪试验解析[J]. 中国岩溶,2017,36(2):226 − 233. [ZHAO Yi,LI Yanqing,QIN Xingming,et al. Tracer tests on distribution and structural characteristics of karst channels in Nandong underground river drainage[J]. Carsologica Sinica,2017,36(2):226 − 233. (in Chinese with English abstract)

    [34]

    谢国文,杨平恒,卢丙清,等. 基于高分辨率示踪技术的岩溶隧道涌水来源识别及含水介质研究[J]. 中国岩溶,2018,37(6):892 − 899. [XIE Guowen,YANG Pingheng,LU Bingqing,et al. Application of high-resolution tracer technique in identifying the source of water gushing and the structure of aquifer medium in karst tunnel[J]. Carsologica Sinica,2018,37(6):892 − 899. (in Chinese with English abstract)

    • 相关文章
  • 施引文献

  • 期刊类型引用(0)

    其他类型引用(2)

    • 资源附件(0)
  • 加载中
    Created with Highcharts 5.0.7访问量Chart context menu近一年内文章摘要浏览量、PDF下载量统计信息摘要浏览量PDF下载量2024-052024-062024-072024-082024-092024-102024-112024-122025-012025-022025-032025-0400.511.522.5Highcharts.com
    Created with Highcharts 5.0.7Chart context menu访问类别分布DOWNLOAD: 2.4 %DOWNLOAD: 2.4 %摘要: 97.6 %摘要: 97.6 %DOWNLOAD摘要Highcharts.com
    Created with Highcharts 5.0.7Chart context menu访问地区分布其他: 26.8 %其他: 26.8 %其他: 0.3 %其他: 0.3 %Seattle: 1.0 %Seattle: 1.0 %[]: 0.6 %[]: 0.6 %上海: 2.6 %上海: 2.6 %北京: 1.0 %北京: 1.0 %台州: 1.0 %台州: 1.0 %哥伦布: 0.3 %哥伦布: 0.3 %天津: 0.6 %天津: 0.6 %常州: 0.3 %常州: 0.3 %武汉: 0.6 %武汉: 0.6 %沈阳: 0.3 %沈阳: 0.3 %深圳: 1.0 %深圳: 1.0 %温州: 0.6 %温州: 0.6 %湖州: 0.3 %湖州: 0.3 %漯河: 1.6 %漯河: 1.6 %石家庄: 0.6 %石家庄: 0.6 %芒廷维尤: 53.5 %芒廷维尤: 53.5 %莫斯科: 2.6 %莫斯科: 2.6 %衢州: 0.6 %衢州: 0.6 %西宁: 1.3 %西宁: 1.3 %贵阳: 1.0 %贵阳: 1.0 %运城: 0.6 %运城: 0.6 %长沙: 0.6 %长沙: 0.6 %其他其他Seattle[]上海北京台州哥伦布天津常州武汉沈阳深圳温州湖州漯河石家庄芒廷维尤莫斯科衢州西宁贵阳运城长沙Highcharts.com

图(8)

表(3)

计量
  • 文章访问数:  655
  • PDF下载数:  43
  • 施引文献:  2
出版历程
收稿日期:  2022-03-22
修回日期:  2022-06-03
录用日期:  2022-10-14
刊出日期:  2023-03-15

目录

摘要
HTML全文

  • 1.1   试验装置

  • 1.2   示踪试验

  • 1.3   室内模型设计相似准则

  • 1.4   穿透曲线分析方法

  • 1.5   模拟方法

  • 2.1   试验结果与分析

  • 2.2   模拟结果与分析

参考文献(34)
相关文章
施引文献
资源附件(0)
版权所有：中国地质调查局发展研究中心 copyright @2020
返回
  • 表 1.  穿透曲线特征参数
    Table 1.  Characteristic parameters of breakthrough curve
    特征参数参数分类计算方法
    Cp最大示踪剂浓度
    Rt示踪剂回收率
    tm水力参数
    v水力参数
    σt2水力参数
    CSK水力参数
    tre水力参数
    t0.5Cp水力参数
    td水力参数
    注：C（t）为在任意t时刻的质量浓度；Q（t）为t时刻的流量；M为示踪剂注入质量。
     | Show Table
    DownLoad: CSV
  • 表 2.  不同管道系统长度的穿透曲线特征参数
    Table 2.  Characteristic parameters of breakthrough curve of the pipe system with different lengths
    水箱结构L/mv/（m·s−1）tm/minσt2/min2CSKtre/st0.5Cp/std/sRt/%
    SP1572.250.4472.70040.157680.14721751218791.97
    83.000.4503.07450.153200.12741641217891.92
    93.750.4583.41240.140150.10971481316192.50
    104.500.4673.73170.109960.08891251313789.27
    ASP1572.250.4462.70160.0523050.0847892010594.99
    83.000.4523.05940.0487100.072282219896.88
    93.750.4573.42270.0450400.062074219091.83
    104.500.4613.77390.0440960.055763217992.36
     | Show Table
    DownLoad: CSV
  • 表 3.  不同管道系统长度的模型参数
    Table 3.  Model parameters of the pipe system with different lengths
    水箱结构L/mD/（m2·s−1）A/m2As/m2α/s−1Vs/m3DaI
    SP1572.251.48×10−24.98×10−44.37×10−55.04×10−33.16×10−313.2
    83.001.33×10−25.00×10−43.89×10−54.26×10−33.23×10−312.6
    93.751.27×10−24.97×10−43.42×10−53.76×10−33.21×10−312.4
    104.501.18×10−24.96×10−42.72×10−53.32×10−32.84×10−313.5
    ASP1572.251.87×10−25.09×10−43.54×10−51.04×10−22.56×10−334.7
    83.001.63×10−25.06×10−43.18×10−51.02×10−22.64×10−337.3
    93.751.57×10−25.08×10−42.67×10−58.44×10−22.50×10−336.5
    104.501.34×10−25.04×10−42.52×10−58.42×10−22.63×10−338.0
     | Show Table
    DownLoad: CSV