Estimation of conductivity fields by using a correlation-based localization scheme of iterative ensemble smoother
-
摘要:
在地下水流和溶质运移问题中，有较多研究基于物理距离局域化集合同化方法反演水文地质参数。当反演参数与观测信息之间不存在物理距离时，这种方法不适用。为了克服这个局限，通过渗透系数与水头信息之间的相关性计算局域化方法的阻滞因子，构建基于相关性的局域化迭代集合平滑方法。为了方便比较，将该方法和一种基于物理距离的局域化迭代集合平滑一同用于同化水头信息反演二维孔隙承压含水层的渗透系数场。算例中考虑了不同集合大小、观测误差及观测数量等因子的组合，便于分析其对渗透系数反演精度的影响。研究结果显示：（1）在所有算例中新方法得到的渗透系数均方根误差范围为[0.8307, 0.9590]，都小于基于物理距离方法的均方根误差，范围为[0.8394, 1.0000]；（2）基于物理距离方法得到的渗透系数场空间上存在不连续性，而新方法的结果不存在此现象。文章提出了一种新的基于相关性局域化迭代平滑方法，该方法不需要依赖参数与观测信息之间的物理距离且参数反演精度高于基于物理距离的方法，可作为参数反演的科学工具。
Abstract:In the studies of groundwater flow and solute transport, many efforts have been made to estimate hydrogeological parameters through physical-distance based localization schemes of ensemble assimilation approaches. However, these methods are unavailable when there are no physical distances between parameters and observations. To avoid this limitation, we calculate the tapering factors in terms of the correlation coefficients between parameters and observations and develop a novel correlation-based localization scheme of iterative ensemble smoother. For the purpose of comparison, a physical distance-based scheme of iterative ensemble smoother together with the new approach are used to assimilate hydraulic head information and estimate the hydraulic conductivity field of a 2D confined aquifer. Among the test cases, we consider different configurations of ensemble size, observation error and number of observations, and their impacts on the accuracy of conductivity estimation can be well explored. The results show that (1) the root mean square error of hydraulic conductivity, RMSE, obtained through the new approach for each test case of interest, is lower than its counterpart through the physical distance-based approach, with the RMSE ranges of [0.8307, 0.9590] and [0.8394, 1.0000] for all test cases through the two approaches, respectively. (2) The estimated conductivity field has discontinuities when using the physical distance-based approach, but this does not happen when using the new approach. In this study, we develop a novel correlation-based localization scheme of iterative ensemble smoother, which is free of the definitions of physical distances between parameters and observations, yields higher accuracy of parameter estimation in comparison with the physical distance-based approach, and can be a useful tool for estimating hydrogeological parameters.
-
集合数据同化方法，包括集合卡尔曼滤波、集合平滑及其迭代形式、粒子滤波等，已被应用于水文地质[1 − 6]、工程地质[7 − 8]、气象[9]、石油工程[10 − 11]等领域。在水文地质领域，集合数据同化方法常被用于反演水文地质参数，包括渗透系数、土壤水动力参数及其他参数。与三维/四维变分方法[12]比较，集合数据同化方法的理论相对简单。由于受计算资源和时间限制，在应用数据同化方法时通常只考虑较小的集合，这会引入参数与观测之间的伪相关性。伪相关性会引起滤波近交甚至滤波发散，影响参数反演精度和观测信息的模拟精度[13]。局域化方法通常被用来削弱伪相关性对参数反演的消极影响。目前，局域化方法按照原理可以分为基于物理距离[14 − 16]和相关性[10 − 12, 17]2种。
基于物理距离的方法是依据参数与观测信息之间的物理距离估计2个变量之间的相关程度，距离越远越不相关，反之越相关。南统超等[16]应用基于物理距离的局域化集合卡尔曼滤波同化水头信息反演一个二维理想孔隙含水层的渗透系数场，结果表明局域化方法能有效消除伪相关性的消极影响，提高渗透系数的反演精度。Tong等[14]研究表明利用集合卡尔曼滤波反演渗透系数时只同化距离较近的水头观测信息有利于削弱伪相关性的消极影响。Xia等[4]利用基于物理距离的局域化迭代集合卡尔曼滤波同化水头和盐度信息，反演海岸带含水层的渗透系数场。基于相关性的方法依据参数与观测信息之间的相关性估计2个变量之间的相关程度，数学定义比基于物理距离的方法更清晰。基于相关性的局域化集合数据同化方法常被用于解决气象预报[18 − 19]和石油开采[10 − 11, 17]问题，专注于地下水问题的研究还比较少。Miyoshi[19]利用基于相关性的局域化集合拓展卡尔曼滤波提高气象预报精度。Luo等[11]和Soares等[17]利用基于相关性的局域化迭代集合平滑反演储油层的渗透率和孔隙度。与基于相关性的局域化比较，基于物理距离的方法存在一个不可避免的缺陷：参数与观测之间必须有明确的物理距离定义。在水文地质领域，有些观测信息和参数没有明确的坐标，比如多含水层的长滤管水头[20]、土壤剖面的水动力参数[21]、流域尺度土壤参数[22]以及含水层尺度的渗透系数和孔隙度[23]等，导致参数与观测信息之间没有明确的物理距离。综上所述，有必要加深对基于相关性局域化方法的研究。
本文提出了一种新的基于相关性的局域化方法并将其与迭代集合平滑方法耦合用于反演一个理想二维孔隙承压含水层的渗透系数场。在算例中，水头观测信息与渗透系数之间存在明确的物理距离。本文同时考虑了基于物理距离的局域化方法，便于分析2种局域化方法的表现。
1. 理论与方法
1.1 地下水流方程
考虑理想二维孔隙承压含水层，非稳定流条件下水头（h）控制方程为[24]：
S∂h(x,t)∂t=∇⋅[K(x)∇h(x,t)]+f(x,t) (1) 式中：S——储水系数；
t——时间；
x——空间位置向量；
∇ ——梯度算子；∇⋅ ——散度算子；K——渗透系数；
f——源汇项。
在本文中，考虑S为定值，K为一个空间随机变量，f为定值。通过局域化迭代集合平滑同化h观测信息反演K。
1.2 局域化迭代集合平滑
参考Luo等[25]的研究，局域化迭代集合平滑的第i次参数更新方程为：
{mi+1=mi+(Ri⊗KiGain)ΔdiKiGain=Sim(Sid)T(Sid(Sid)T+γiI)−1Δdi≡g(mi)−dobsγi = ξitrace(Sid(Sid)T)/O (2) 式中：
m = [m1,m2,⋯,mP]T ——参数向量；P——参数总数；
R ——阻滞矩阵（P×O）；R⊗KGain ——矩阵R 与KGain 的舒尔积；Sm 、Sd ——参数异常矩阵（P×N）、观测信息异常 矩阵（O×N）；ξi ——Levenberg-Marquart算法中自动调整的系数，调整方法与Luo等[10]相同；I——O×O的单位矩阵；
g(⋅) ——模型-观测算子；dobs=[d1obs,d2obs,…,dOobs]T ——观测向量；O——观测信息总数。
在本文中，
dobs 包含了所有的水头观测信息，m 包含了含水层不同位置的渗透系数。本文设置2点迭代集合平滑收敛的依据：（1）达到最大迭代次数；
（2）连续2次迭代之间参数向量之差的二范小于设定的阈值。
不同局域化方法得到不同阻滞矩阵
(R) ，R⊗KGain 使得与参数相关度高的观测信息才能用于更新参数。R 中第k行s列的元素被称为阻滞因子(rks) ，通过阻滞函数得到。与大多数研究[14 − 15, 26]相同，本文中的阻滞函数为阻滞函数的输入与阻滞因子之间的映射关系。本文选取Gaspari-Cohn函数为阻滞函数[10, 26]：
rks=fGC(zks)={−14z5ks+12z4ks+58z3ks−53z2ks+10⩽ (3) Gaspari-Cohn函数的输入
{\textit{z}_{ks}} 不同得到的{r_{ks}} 也不同。基于物理距离和相关性的局域化方法，由于其机理不同，它们对应的{\textit{z}_{ks}} 表达式理论上不相同。1.3 基于物理距离的局域化
参考Xia等[4]和Nan等[15]，基于物理距离的局域化方法考虑阻滞函数输入
{\textit{z}_{ks}} 为：\left\{ {\begin{split} &{{\textit{z}_{ks}} = 3\left( {\frac{{{d_1}}}{{{\beta _1}}} + \frac{{{d_2}}}{{{\beta _2}}}} \right)} \\ &{{\beta _i} = {\delta _i}{{\left( {\sqrt {9 + 8N} - 5} \right)} / 4}} \\ &{{\delta _i} = {\lambda _i}/2} \end{split}} \right. (4) 式中：
{d_i} ——两空间位置（这里指第s个观测信息与第 k个参数的空间位置）在xi方向的距离，i = 1, 2；{\beta _i} ——在xi方向的阻滞关键长度，i = 1, 2（参见文献[4, 18]）；{\lambda _i} ——在xi方向的渗透系数相关长度，i = 1, 2。为了便于表达，基于物理距离的局域化迭代集合平滑被记为DL_iES。
1.4 基于相关性的局域化
假定
{\textit{z}_{ks}} 与相关系数（{\rho _{ks}} ）满足椭圆方程：\left\{ {\begin{split} &{\frac{{\textit{z}_{ks}^2}}{{{1 /{{{\left( {1 - w} \right)}^2}}}}} + {\rho _{ks}}^2 = 1,{\text{ }}0 \leqslant {\textit{z}_{ks}}} \\ &{{\rho _{ks}} = \frac{{\displaystyle\sum_{i = 1}^N {\left( {m_{k,i}^{} - \bar m_k^{}} \right)\left( {y_{s,i}^{{\text{RS}}} - \bar y_s^{{\text{RS}}}} \right)} }}{{N{\sigma _{{\text{m}}_k^{}}}{\sigma _{{\text{y}}_s^{{\text{RS}}}}}}}} \end{split}} \right. (5) 式中：
\bar m_k^{} ——第k个参数变量的集合均值；\bar y_s^{{\text{RS}}} ——第s个观测变量的集合均值；{\sigma _{{\text{m}}_k^{}}} ——参数变量m_k^{} 的标准差；{\sigma _{{\text{y}}_s^{{\text{RS}}}}} ——观测变量y_s^{{\text{RS}}} 的标准差。由式（5）可得
{\textit{z}_{ks}} 的表达式为：{\textit{z}_{ks}} = \varphi \left( {{\rho _{ks}}} \right) = \frac{{\sqrt {1 - {\rho _{ks}}^2} }}{{1 - w}} (6) 式中：
w ——观测水头与渗透系数不相关时相关系数 的高斯白噪音阈值，0<w <1。依据Anderson[27]的研究，本文定义
w 的表达式为：w = \frac{\alpha }{{\sqrt N }} (7) 式中：α——相关系数白噪音标准差(
{1 /{\sqrt N }} [27])的倍数， 0<α<\sqrt N 。依据高斯分布的概率密度函数，通常取1，2或3个标准差表示白噪音水平。本文将
{\textit{z}_{ks}} 与{\rho _{ks}} 之间映射关系描述为椭圆方程。当\left| {{\rho _{ks}}} \right| = 1 时，认为参数与观测信息之间高度相关，{r_{ks}} = {f_{{\text{GC}}}}\left( {g\left( 1 \right)} \right) = 1 。当\left| {{\rho _{ks}}} \right| < w 时，认为参数与观测信息之间相关性很弱，不同化第s个观测信息用于反演含水层的第k个渗透系数，即{r_{ks}} = 0 。综上，本文用于计算阻滞因子({r_{ks}}) 的表达式为：{r_{ks}} = \left\{ {\begin{array}{*{20}{c}} {{f_{{\text{GC}}}}\left( {\varphi \left( {{\rho _{ks}}} \right)} \right)} \\ 0 \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {w \leqslant \left| {{\rho _{ks}}} \right|} \\ {\left| {{\rho _{ks}}} \right| \lt w} \end{array} (8) 从式（8）可推得：
（1）当N较小时，
{\textit{z}_{ks}} 应该取较大的值（即椭圆的长轴半径a ={1 \mathord{\left/ {\vphantom {1 {\left( {1 - w} \right)}}} \right. } {\left( {1 - w} \right)}} , 1 < a < ∞）使得阻滞函数得到较小的{r_{ks}} 。（2）当N很大（比如
N \to \infty ）时，{\textit{z}_{ks}} = \varphi \left( {{\rho _{ks}}} \right) = \sqrt {1 - \rho _{ks}^2} 不恒等于1。理论层面上，当N \to \infty 时，局域化方法应该满足{r_{ks}} \equiv 1 。但是，局域化方法只用于N较小的情况（通常N取值为50，100，300，500等），对新方法的普适性影响较小。为了便于表达，将本文提出的基于相关性的局域化迭代集合平滑记为CL_iES。2. 算例
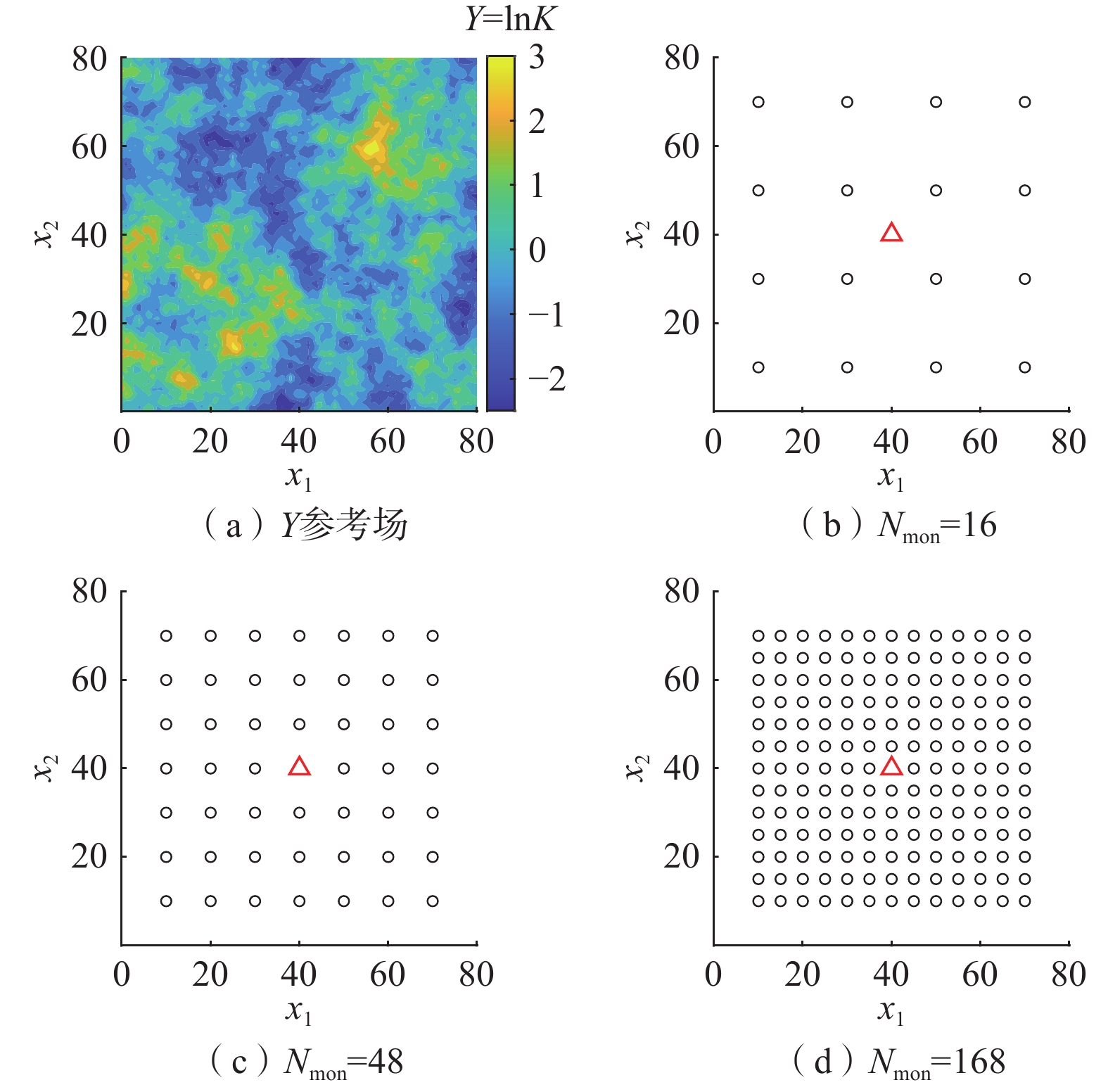
本文考虑二维承压孔隙含水层的渗透系数场反演作为算例。含水层大小为80×80（全文单位保持一致，本文剩余部分省略单位描述）。含水层左右2侧x1 = 0，80处分别为给定水头边界h = 1，0，上下2侧x2 = 0 ，80为隔水边界，中心处（x1 = 40，x2 = 40）设置一口井（图1），抽水率恒定为2。含水层的初始水头为不抽水情况下含水层的稳定水头。含水层储水系数为0.001。非稳定地下水流模型的总模拟时长为4，被均匀地分为20个应力期。数值模型采用标准有限元法求解（参见文献[20]）。将含水层空间等距离散为81×81（P = 6561）的节点网格。渗透系数的对数（Y = lnK）为服从高斯分布的空间随机变量，用指数协方差函数刻画渗透系数空间变异性：
图 1. Y参考场和16，48，168口监测井空间分布图Figure 1. Y reference field and spatial distribution of 16, 48 and 168 monitoring wellsC_{\text{Y}}^{} = \sigma _{\text{Y}}^2\exp \left( { - \frac{1}{2}\left[ {\frac{{{d_1}}}{{{\lambda _1}}} + \frac{{{d_2}}}{{{\lambda _2}}}} \right]} \right) (9) 式中：
\sigma _{\text{Y}}^2 ——渗透系数的方差。算例只考虑渗透系数为随机变量，其余参数和边界条件设置为已知。使用均值0.0和方差1.0生成的Y参考场见图1（a）。此外，使用均值0.5和方差1.0生成初始Y场的集合。Y参考场与初始Y场的渗透系数具有相同的相关长度，
{\lambda _1} = {\lambda _2} = 8 。以Y参考场作为模型的输入获得的水头场被称为参考水头场。观测水头通过监测井的参考水头加上标准差为{\sigma _{{\text{obs}}}} 的高斯白噪音得到。每个应力期的每口监测井都提供观测信息。2种方法（即DL_iES和CL_iES）在迭代过程中使用的参数相同。具体包括：Levenberg-Marquart算法中初始系数
({\xi ^0}) 设置为20；迭代集合平滑的最大迭代次数为20，连续2次迭代之间参数向量之差的二范小于1×10−6时迭代停止。在算例中，除了集合大小(N)、水头观测误差的标准差
({\sigma _{{\text{obs}}}}) 、监测井数量(Nmon)及相关系数白噪音标准差的倍数(α)的取值有变化，其余设置与以上描述相同。采用控制变量法研究N、{\sigma _{{\text{obs}}}} 、Nmon及α的取值对渗透系数反演精度的影响。具体描述如下：第1组试验，设定{\sigma _{{\text{obs}}}} =0.01、Nmon = 48 （即O = 960）、α = 2，N的取值为50，100，500；第2组，设定N = 100、Nmon = 48、α = 2，{\sigma _{{\text{obs}}}} 的取值为0.1，0.01，0.001；第3组，设定N = 100、{\sigma _{{\text{obs}}}} =0.01、α = 2，考虑Nmon = 16（即O = 320，图1b），48（即O = 960，图1c），168（即O = 3360，图1d）；第4组，设定N = 100、{\sigma _{{\text{obs}}}} = 0.01、Nmon = 48，α的取值为1.0，1.5，2.0，2.5，3.0。使用渗透系数的均方根误差(RMSE)和水头的绝对误差(Eh)定量评价2种方法的表现。RMSE与Eh的表达式分别为：
R_{{\rm{MSE}}} = \sqrt {\frac{1}{P}{{\sum_j^P {\left( {Y_j^{{\text{ref}}} - {{\left\langle {Y_j^{}} \right\rangle }^{{\text{est}}}}} \right)} }^2}} (10) {E_{\text{h}}} = \frac{1}{P}\sum_j^P {\left| {h_j^{{\text{ref}}} - {{\left\langle {{h_j}} \right\rangle }^{{\text{up}}}}} \right|} (11) 式中：
Y_j^{{\text{ref}}} 、{\left\langle {Y_j^{}} \right\rangle ^{{\text{est}}}} ——j节点Y参考值、在该节点的Y估 计值；h_j^{{\text{ref}}} 、{\left\langle {{h_j}} \right\rangle ^{{\text{up}}}} ——j节点上的参考水头、更新水头。Y反演场的标准差(SY)，常用于定量Y集合内部的差异性，其表达式为：
{S_{\text{Y}}} = \sqrt {\frac{1}{P}\sum\limits_{j = 1}^P {{{\left( {\sigma _{{{\text{Y}}_j}}^2} \right)}^{{\text{est}}}}} } (12) 式中：
{\left( {\sigma _{{{\text{Y}}_j}}^2} \right)^{{\text{est}}}} ——第j个节点处Y方差的估计值。3. 结果
3.1 集合大小的影响（第1组）
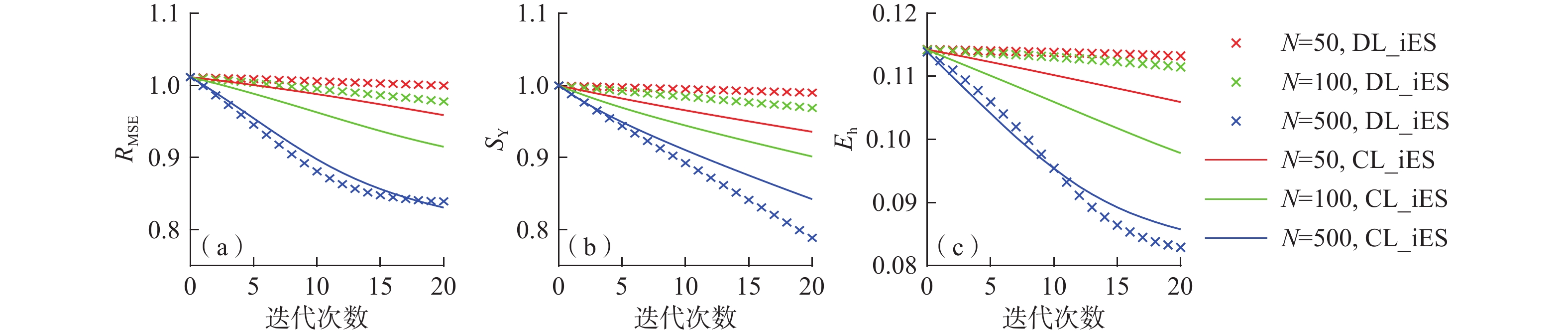
图2展示N = 50，100，500时由DL_iES和CL_iES得到RMSE（图2a）、SY（图2b）及Eh（图2c）随迭代次数变化的曲线。当N由50增大到100时，DL_iES得到的RMSE、SY及Eh值的变化幅度比由CL_iES得到变化幅度小。随着N增大，DL_iES和CL_iES得到的RMSE、SY及Eh总体展现下降趋势。当集合大小相同时，CL_iES得到的RMSE和Eh总体都要低于DL_iES得到的值，特别是当集合较小（即N = 50或100）时。
图 2. 由DL_iES和CL_iES在N = 50，100，500时得到的RMSE、SY和Eh随迭代次数变化的曲线Figure 2. Changes of RMSE, SY and Eh obtained through DL_iES and CL_iES with iteration timeswhen N = 50, 100, 500与图2相对应，表1列出DL_iES和CL_iES第20次迭代得到的RMSE、SY及Eh值。随着集合增大，DL_iES和CL_iES对应的渗透系数反演误差和水头模拟误差均减小，前者对应的误差基本高于后者。综合RMSE与SY结果，2种方法都能维持Y集合内部的差异性和能有效减小伪相关性对反演渗透系数的消极影响。
表 1. 第1组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值Table 1. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 1 at the 20th iteration参数 模型 集合大小 50 100 500 RMSE DL_iES 1.0000 0.9779 0.8394 CL_iES 0.9590 0.9151 0.8307 SY DL_iES 0.9901 0.9689 0.7887 CL_iES 0.9359 0.9016 0.8424 Eh DL_iES 0.1132 0.1115 0.0829 CL_iES 0.1059 0.0978 0.0858 | Show Table
DownLoad:
CSV
图3绘制了第1组中DL_iES和CL_iES在第20次迭代后得到的Y估计场和对应的Y方差（
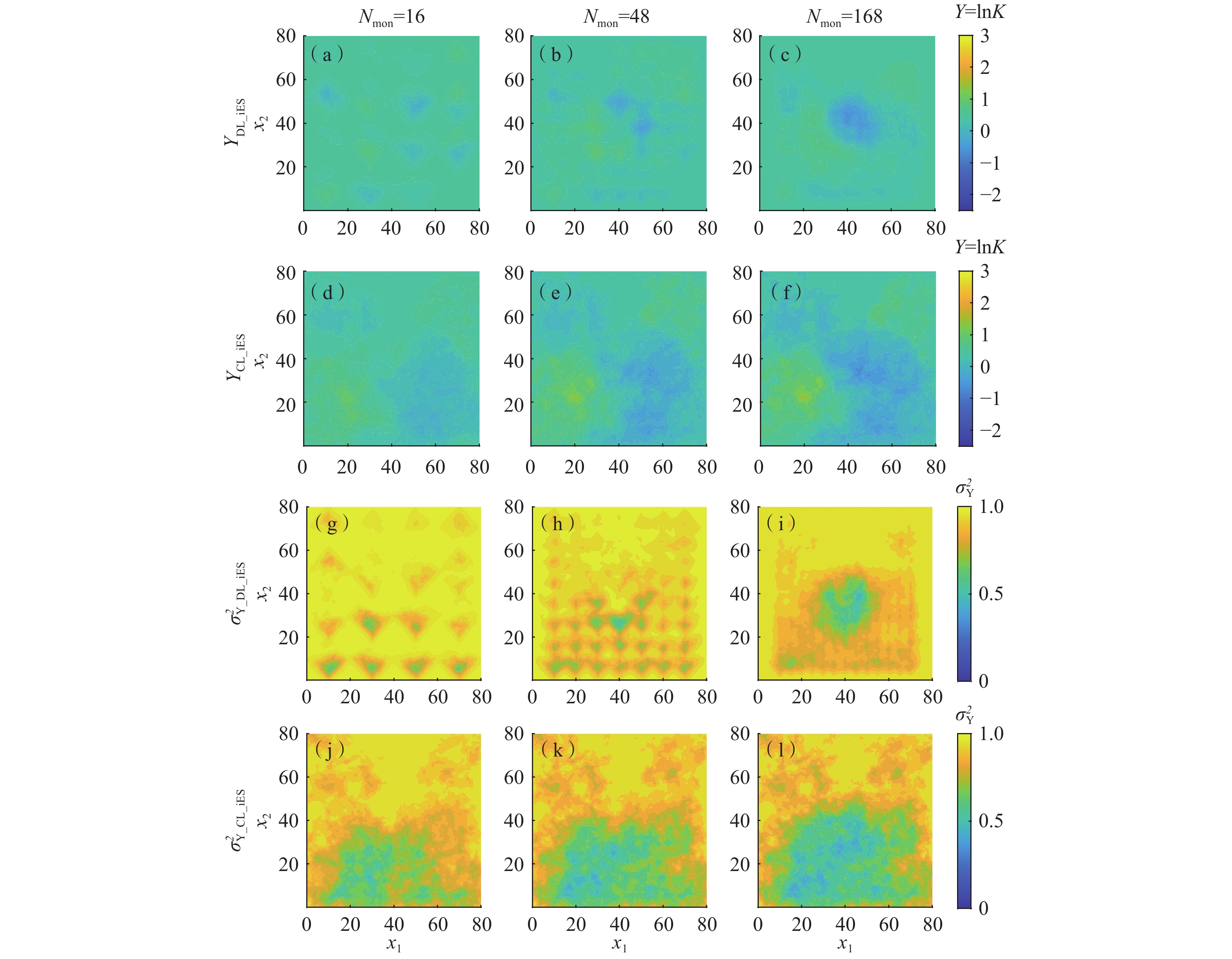
\sigma _{\text{Y}}^2 ）估计场。从图3中可以看出：
图 3. 当N = 50，100，500时，通过DL_iES和CL_iES在第20次迭代后获得的Y估计场和Y方差(\sigma _{\text{Y}}^2 )估计场Figure 3. Maps of Y fields and Y variance(\sigma _{\text{Y}}^2) estimated through DL_iES and CL_iES at the 20th iteration when N = 50, 100, 500（1）当N = 50或100时，DL_iES得到的反演结果空间上出现不连续性，而CL_iES则无此现象，且CL_iES得到的结果更接近Y参考场，见图1（a）。
（2）当N = 500时，2种方法得到Y和
\sigma _{\text{Y}}^{\text{2}} 估计场都较为相似，接近参考场。DL_iES得到的\sigma _{\text{Y}}^{\text{2}} 估计场出现规律的不连续性随着N增大而逐渐消失。当N相同时，DL_iES和CL_iES得到的\sigma _{\text{Y}}^{\text{2}} 估计场总体相近，均是介于下边界和抽水井的区域值较低，而介于上边界和抽水井的区域值较高。综合以上结果，当考虑不同集合时CL_iES具有良好自适应性，且表现优于DL_iES。
3.2 观测误差的影响（第2组）
第2组中DL_iES和CL_iES第20次迭代得到的RMSE、SY及Eh值，见表2。随着
{\sigma _{{\text{obs}}}} 由0.001增大到0.1，RMSE和SY总体上变化不大，而Eh呈现明显的递增趋势。造成这一现象的原因是渗透系数反演过程存在多解性。这些结果说明局域化方法在应对观测误差变化时，也具有较好的适应能力。与DL_iES相比，CL_iES得到的RMSE和Eh更低。表 2. 第2组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值Table 2. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 2 at the 20th iteration参数 模型 观测误差 0.1 0.01 0.001 RMSE DL_iES 0.9744 0.9779 0.9801 CL_iES 0.9187 0.9151 0.9162 SY DL_iES 0.9691 0.9689 0.9690 CL_iES 0.9029 0.9016 0.9015 Eh DL_iES 0.2728 0.1115 0.0789 CL_iES 0.2677 0.0978 0.0571 | Show TableDownLoad:
CSV
综合以上结果，当考虑不同
{\sigma _{{\text{obs}}}} 时CL_iES具有良好的自适应性，且表现优于DL_iES。3.3 观测数量的影响（第3组）
第3组中DL_iES和CL_iES第20次迭代得到的RMSE、SY及Eh值如表3所示。随着Nmon增大，渗透系数反演精度增高（即RMSE减小）而水头模拟精度没有出现明显变化。造成这一现象的原因是渗透系数反演过程存在多解性。水头很可能不会对所有位置的渗透系数都敏感。
表 3. 第3组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值Table 3. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 3 at the 20th iteration参数 模型 观测数量 16 48 168 RMSE DL_iES 0.9999 0.9779 0.9575 CL_iES 0.9537 0.9151 0.8974 SY DL_iES 0.9862 0.9689 0.9543 CL_iES 0.9281 0.9016 0.8850 Eh DL_iES 0.1023 0.1115 0.1090 CL_iES 0.0948 0.0978 0.0932 | Show TableDownLoad:
CSV
与图3相似，图4绘制第3组中DL_iES和CL_iES第20次迭代得到的Y和
\sigma _{\text{Y}}^2 估计场。当Nmon = 16或48时，DL_iES得到的Y和\sigma _{\text{Y}}^2 估计场在空间上呈现不连续性；而当Nmon = 168时，这种不连续性有所减弱。CL_iES得到的Y和\sigma _{\text{Y}}^2 估计场无此现象。随着Nmon增大，CL_iES得到的Y估计场逐渐逼近Y参考场。综合以上结果表明当考虑不同Nmon时CL_iES具有良好自适应性，且表现优于DL_iES。3.4 相关系数高斯白噪音阈值的影响（第4组）
第4组中CL_iES第20次迭代得到的RMSE、SY及Eh值如表4所示。随着相关系数白噪音阈值的增大（即α由1.0增大到3.0），RMSE、SY及Eh值都呈现明显的增大趋势。使用CL_iES时，设置1个较大白噪音阈值可以削弱更多相关系数噪音对渗透系数反演的影响，但同时也增大算法整体阻滞强度，所以RMSE、SY及Eh值都呈现明显的增大趋势。这些结果指示CL_iES在应对相关系数高斯白噪音的不同阈值时能做出合理的响应。
表 4. 第4组第20次迭代后CL_iES得到的RMSE、SY和Eh值Table 4. Final values of RMSE, SY and Eh through CL_iES for Group 4 at the 20th iteration参数 相关系数高斯白噪音标准差的倍数 1.0 1.5 2.0 2.5 3.0 RMSE 0.8782 0.8920 0.9151 0.9443 0.9706 SY 0.8367 0.8715 0.9016 0.9273 0.9500 Eh 0.0901 0.0936 0.0978 0.1027 0.1071 | Show TableDownLoad:
CSV
4. 讨论
DL_iES和CL_iES在应对不同集合大小、观测信息误差和监测井数目时都表现良好。与DL_iES相比，CL_iES得到渗透系数反演和水头模拟精度都要更高。这是因为CL_iES的局域化基于渗透系数与观测水头之间的相关系数，而DL_iES基于渗透系数与观测水头之间的物理距离。CL_iES在进行局域化的过程中考虑了渗透系数与观测水头之间的相关性。这样可以避免基于物理距离局域化方法（包括DL_iES）的重要不足：在计算阻滞因子时假定渗透系数与观测水头之间相关关系与物理距离成正比，且物理距离远近能够完美地反映相关性大小。在计算过程中将最靠近点（0，0）的监测井，在第1个时间步长的观测水头设为第1个观测信息。该水头与Y的相关系数为
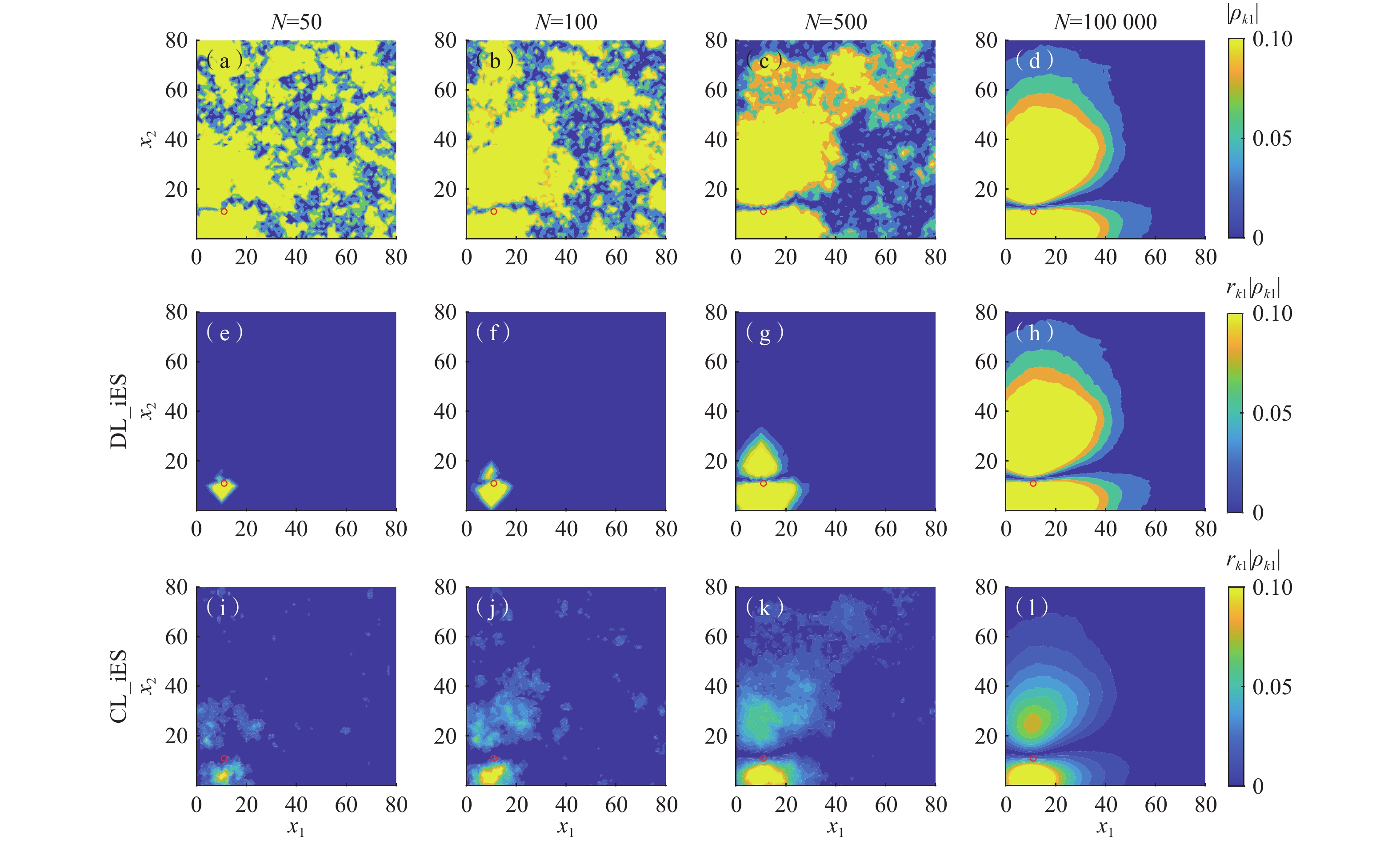
{\rho _{k1}} （k = 1，2，···，6561）。图5展示N = 50，100，500，100000时{\rho _{k1}} 的绝对值\left| {{\rho _{k1}}} \right| 分布和通过DL_iES和CL_iES获得的对应的阻滞绝对值{r_{k1}}\left| {{\rho _{k1}}} \right| （k = 1，2，···，6561）的分布。Xia 等[20]研究显示当N = 10000时伪相关性基本消失。基于此，N = 100000对应的相关系数场噪音很小，本研究将其设定为真实的相关系数空间分布。图5（a）—（d）展示：（1）\left| {{\rho _{k1}}} \right| 在空间上总体越靠近监测井值越大，随着N增大到100000，这种现象更加明显；（2）有相当多的位置距离监测井近但\left| {{\rho _{k1}}} \right| 值低，同时也有较多的位置离监测井相对较远但渗透系数与水头之间存在相关性。图5（d）—（f）展示DL_iES获得的{r_{k1}}\left| {{\rho _{k1}}} \right| 分布图。随着N增大，以监测井为中心{r_{k1}}\left| {{\rho _{k1}}} \right| 不为0的范围也增大，当N增大到100000时，{r_{k1}}\left| {{\rho _{k1}}} \right| 接近\left| {{\rho _{k1}}} \right| ，这是合理的。依据式（4），图5（f）对应的{r_{k1}} 取值范围为[0.7123, 0.9926]。图5（i）—（l）展示CL_iES获得的{r_{k1}}\left| {{\rho _{k1}}} \right| 分布图。与DL_iES相比，CL_iES对应的{r_{k1}}\left| {{\rho _{k1}}} \right| 的空间分布相对不规则，但不为0的值总体也集中在监测井附近。CL_iES能够考虑到渗透系数与水头之间物理距离大但又具有相关性的情况，也能考虑物理距离小但相关性微弱甚至没有的情况。基于相关性局域化方法在数学理论上比基于物理距离的局域化方法更合理，数理意义更加清晰。
图 5. 当N = 50，100，500和100000的\left| {{\rho _{k1}}} \right| 及{r_{k1}}\left| {{\rho _{k1}}} \right| 分布图注：图中红色圆圈代表最靠近点（0，0）的监测井位置为观测水头的固定点。Figure 5.\left| {{\rho _{k1}}} \right| and{r_{k1}}\left| {{\rho _{k1}}} \right| maps considering N = 50, 100, 500, 100000由图5可知CL_iES比较明显的缺陷有2个：
（1）当N从50增大到500，有些零星的伪相关性难以被去除。
（2）当N =100000时，因为
{r_{k1}} 值总体不接近于1，{r_{k1}}\left| {{\rho _{k1}}} \right| 的空间分布差异明显，见图5（l）与图5（d）。这2点都指示式（8）并不能完美地刻画
{r_{ks}} 与{\rho _{ks}} 之间的映射关系。依据RMSE与SY的结果（表1—3），缺陷（1）并没有很大程度削弱Y集合内部的差异性和Y的反演精度。此外，通过增大白噪音阈值(w) ，理论上可适当削弱这些零星的伪相关性。缺陷（2）与1.4节的阐述相同，实际应用过程中受计算成本限制，一般只考虑较小的N。所以缺陷（2）对CL_iES方法的普适性影响较小。5. 结论
本文提出了一种基于相关性的局域化迭代集合平滑方法（记为CL_iES）。将CL_iES与一种基于物理距离的局域化迭代集合平滑（记为DL_iES）用于反演二维孔隙承压含水层的渗透系数场。分析了不同集合大小、观测误差、观测数量及相关系数白噪音阈值条件下CL_iES与DL_iES在反演渗透系数场方面的表现。基于理论推演与算例结果，对CL_iES方法的优劣进行了分析和讨论。
（1）CL_iES是一种有效可靠的反演方法。在不同集合大小、水头观测误差和观测数目等条件下，CL_iES均得到合理的渗透系数反演结果。随着集合增大，CL_iES得到的渗透系数反演精度逐步提高。
（2）由CL_iES反演得到的渗透系数场的精度高于DL_iES得到的结果。在不同集合大小、水头观测误差和观测数目等条件下，CL_iES得到渗透系数反演和水头模拟精度都要高于DL_iES。此外，由DL_iES得到渗透系数及其方差在较小集合和观测数目条件下均出现了空间上斑状不连续现象，而DL_iES不存在此现象。
（3）基于物理距离的局域化迭代集合平滑方法依据参数与观测信息的物理距离定量二者之间的相关程度，局域化的效果受阻滞函数和阻滞关键长度影响。与基于物理距离的方法相比，基于相关性的局域化方法依据参数与观测信息之间的相关性定量二者之间的相关程度，数学意义更清晰，且不需要二者之间存在物理距离定义。在未来研究中，值得更加关注利用基于相关性的局域化集合数据同化方法反演水文地质参数。
-
图 3 当N = 50，100，500时，通过DL_iES和CL_iES在第20次迭代后获得的Y估计场和Y方差(
\sigma _{\text{Y}}^2 )估计场Figure 3.
图 4 在Nmon = 16，48，168时，通过DL_iES和CL_iES在第20次迭代后获得的Y估计场和Y方差(
\sigma _{\text{Y}}^2 )估计场Figure 4.
图 5 当N = 50，100，500和100000的
\left| {{\rho _{k1}}} \right| 及{r_{k1}}\left| {{\rho _{k1}}} \right| 分布图Figure 5.
表 1 第1组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值
Table 1. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 1 at the 20th iteration
参数 模型 集合大小 50 100 500 RMSE DL_iES 1.0000 0.9779 0.8394 CL_iES 0.9590 0.9151 0.8307 SY DL_iES 0.9901 0.9689 0.7887 CL_iES 0.9359 0.9016 0.8424 Eh DL_iES 0.1132 0.1115 0.0829 CL_iES 0.1059 0.0978 0.0858
下载: 导出CSV
表 2 第2组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值
Table 2. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 2 at the 20th iteration
参数 模型 观测误差 0.1 0.01 0.001 RMSE DL_iES 0.9744 0.9779 0.9801 CL_iES 0.9187 0.9151 0.9162 SY DL_iES 0.9691 0.9689 0.9690 CL_iES 0.9029 0.9016 0.9015 Eh DL_iES 0.2728 0.1115 0.0789 CL_iES 0.2677 0.0978 0.0571
下载: 导出CSV
表 3 第3组第20次迭代后DL_iES和CL_iES得到的RMSE、SY和Eh值
Table 3. Final values of RMSE, SY and Eh through DL_iES and CL_iES for Group 3 at the 20th iteration
参数 模型 观测数量 16 48 168 RMSE DL_iES 0.9999 0.9779 0.9575 CL_iES 0.9537 0.9151 0.8974 SY DL_iES 0.9862 0.9689 0.9543 CL_iES 0.9281 0.9016 0.8850 Eh DL_iES 0.1023 0.1115 0.1090 CL_iES 0.0948 0.0978 0.0932
下载: 导出CSV
表 4 第4组第20次迭代后CL_iES得到的RMSE、SY和Eh值
Table 4. Final values of RMSE, SY and Eh through CL_iES for Group 4 at the 20th iteration
参数 相关系数高斯白噪音标准差的倍数 1.0 1.5 2.0 2.5 3.0 RMSE 0.8782 0.8920 0.9151 0.9443 0.9706 SY 0.8367 0.8715 0.9016 0.9273 0.9500 Eh 0.0901 0.0936 0.0978 0.1027 0.1071
下载: 导出CSV
-
[1] 杨运,吴吉春,骆乾坤,等. 考虑预报偏差的迭代式集合卡尔曼滤波在地下水水流数据同化中的应用[J]. 水文地质工程地质,2022,49(6):13 − 23. [YANG Yun,WU Jichun,LUO Qiankun,et al. Application of the bias aware Ensemble Kalman Filter with confirming option (Bias-CEnKF) in groundwater flow data assimilation[J]. Hydrogeology & Engineering Geology,2022,49(6):13 − 23. (in Chinese with English abstract)
YANG Yun, WU Jichun, LUO Qiankun, et al . Application of the bias aware Ensemble Kalman Filter with confirming option （Bias-CEnKF） in groundwater flow data assimilation[J]. Hydrogeology & Engineering Geology,2022 ,49 （6 ）:13 −23 . （in Chinese with English abstract）[2] 宗成元,康学远,施小清,等. 基于多点地质统计与集合平滑数据同化方法识别非高斯渗透系数场[J]. 水文地质工程地质,2020,47(2):1 − 8. [ZONG Chengyuan,KANG Xueyuan,SHI Xiaoqing,et al. Characterization of non-Gaussian hydraulic conductivity fields using multiple-point geostatistics and ensemble smoother with multiple data assimilation method[J]. Hydrogeology & Engineering Geology,2020,47(2):1 − 8. (in Chinese with English abstract)
ZONG Chengyuan, KANG Xueyuan, SHI Xiaoqing, et al . Characterization of non-Gaussian hydraulic conductivity fields using multiple-point geostatistics and ensemble smoother with multiple data assimilation method[J]. Hydrogeology & Engineering Geology,2020 ,47 （2 ）:1 −8 . （in Chinese with English abstract）[3] MO Shaoxing,ZABARAS N,SHI Xiaoqing,et al. Deep autoregressive neural networks for high-dimensional inverse problems in groundwater contaminant source identification[J]. Water Resources Research,2019,55(5):3856 − 3881. doi: 10.1029/2018WR024638
[4] XIA Chuanan,HU B X,TONG Juxiu,et al. Data assimilation in density-dependent subsurface flows via localized iterative ensemble Kalman filter[J]. Water Resources Research,2018,54(9):6259 − 6281. doi: 10.1029/2017WR022369
[5] ZHANG Jiangjiang,LIN Guang,LI Weixuan,et al. An iterative local updating ensemble smoother for estimation and uncertainty assessment of hydrologic model parameters with multimodal distributions[J]. Water Resources Research,2018,54(3):1716 − 1733. doi: 10.1002/2017WR020906
[6] CHEN Zi,GÓMEZ-HERNÁNDEZ J J,XU Teng,et al. Joint identification of contaminant source and aquifer geometry in a sandbox experiment with the restart ensemble Kalman filter[J]. Journal of Hydrology,2018,564:1074 − 1084. doi: 10.1016/j.jhydrol.2018.07.073
[7] 李丽敏,温宗周,董勋凯,等. 基于矩阵奇异值分解约束型无迹粒子滤波的滑坡位移预测模型研究[J]. 水土保持通报,2019,39(1):132 − 136. [LI Limin,WEN Zongzhou,DONG Xunkai,et al. Landslide displacement prediction model based on singular value decomposition constrained unscented particle filter[J]. Bulletin of Soil and Water Conservation,2019,39(1):132 − 136. (in Chinese with English abstract)
LI Limin, WEN Zongzhou, DONG Xunkai, et al . Landslide displacement prediction model based on singular value decomposition constrained unscented particle filter[J]. Bulletin of Soil and Water Conservation,2019 ,39 （1 ）:132 −136 . （in Chinese with English abstract）[8] 薛长虎. 基于改进粒子滤波的大型滑坡数据同化方法研究[D]. 武汉:武汉大学,2019 [XUE Changhu. Research on data assimilation method of large landslide based on improved particle filter[D]. Wuhan:Wuhan University,2019. (in Chinese with English abstract)
XUE Changhu. Research on data assimilation method of large landslide based on improved particle filter[D]. Wuhan: Wuhan University, 2019. （in Chinese with English abstract） [9] ZHANG Hongqin,TIAN Xiangjun. A multigrid nonlinear least squares four-dimensional variational data assimilation scheme with the advanced research weather research and forecasting model[J]. Journal of Geophysical Research:Atmospheres,2018,123(10):5116 − 5129.
[10] LUO Xiaodong,BHAKTA T. Automatic and adaptive localization for ensemble-based history matching[J]. Journal of Petroleum Science and Engineering,2020,184:106559. doi: 10.1016/j.petrol.2019.106559
[11] LUO Xiaodong,LORENTZEN R,VALESTRAND R,et al. Correlation-based adaptive localization for ensemble-based history matching:applied to the norne field case study[Z]. Spe Norway One Day Seminar,Norway,2018.
[12] BISHOP C H,HODYSS D. Adaptive ensemble covariance localization in ensemble 4D-VAR state estimation[J]. Monthly Weather Review,2011,139(4):1241 − 1255. doi: 10.1175/2010MWR3403.1
[13] CHEN Yan,ZHANG Dongxiao. Data assimilation for transient flow in geologic formations via ensemble Kalman filter[J]. Advances in Water Resources,2006,29(8):1107 − 1122. doi: 10.1016/j.advwatres.2005.09.007
[14] TONG Juxiu,HU B X,YANG Jinzhong. Assimilating transient groundwater flow data via a localized ensemble Kalman filter to calibrate a heterogeneous conductivity field[J]. Stochastic Environmental Research and Risk Assessment,2012,26(3):467 − 478. doi: 10.1007/s00477-011-0534-0
[15] NAN Tongchao,WU Jichun. Groundwater parameter estimation using the ensemble Kalman filter with localization[J]. Hydrogeology Journal,2011,19(3):547 − 561. doi: 10.1007/s10040-010-0679-9
[16] 南统超,吴吉春. 集合卡尔曼滤波估计水文地质参数的局域化修正[J]. 水科学进展,2010,21(5):613 − 621. [NAN Tongchao,WU Jichun. Localization corrections for the estimation of hydrogeological parameters using ensemble Kalman filter[J]. Advances in Water Science,2010,21(5):613 − 621. (in Chinese with English abstract)
NAN Tongchao, WU Jichun . Localization corrections for the estimation of hydrogeological parameters using ensemble Kalman filter[J]. Advances in Water Science,2010 ,21 （5 ）:613 −621 . （in Chinese with English abstract）[17] SOARES R V,MASCHIO C,SCHIOZER D J. A novel localization scheme for scalar uncertainties in ensemble-based data assimilation methods[J]. Journal of Petroleum Exploration and Production Technology,2019,9(4):2497 − 2510. doi: 10.1007/s13202-019-0727-5
[18] FURRER R,BENGTSSON T. Estimation of high-dimensional prior and posterior covariance matrices in Kalman filter variants[J]. Journal of Multivariate Analysis,2007,98(2):227 − 255. doi: 10.1016/j.jmva.2006.08.003
[19] MIYOSHI T. An adaptive covariance localization method with the LETKF[C]//14th Symposium on Integrated Observing and Assimilation Systems for the Atmosphere,Oceans,and Land Surface (IOAS-AOLS). Atlanta:Americian Meterological Society,2010.
[20] XIA Chuanan,LUO Xiaodong,HU B X,et al. Data assimilation with multiple types of observation boreholes via the ensemble Kalman filter embedded within stochastic moment equations[J]. Hydrology and Earth System Sciences,2021,25(4):1689 − 1709. doi: 10.5194/hess-25-1689-2021
[21] SONG Xuehang,SHI Liangsheng,YE Ming,et al. Numerical comparison of iterative ensemble Kalman filters for unsaturated flow inverse modeling[J]. Vadose Zone Journal,2014,13(2):1 − 12.
[22] 周研来,郭生练,郭家力,等. VIC模型参数的地区分布规律及在无资料流域的移用[J]. 水资源研究,2012,1(3):56 − 63. [ZHOU Yanlai,GUO Shenglian,GUO Jiali,et al. Regional distribution of the VIC model parameters and application in ungauged basins [J]. Journal of Water Resources Research,2012,1(3):56 − 63 (in Chinese with English Abstrct)
ZHOU Yanlai, GUO Shenglian, GUO Jiali, et al . Regional distribution of the VIC model parameters and application in ungauged basins [J]. Journal of Water Resources Research,2012 ,1 （3 ）:56 −63 （in Chinese with English Abstrct）[23] 石鸿蕾,郝奇琛,邵景力,等. 基于多源数据的弱透水层水文地质参数反演研究——以呼和浩特盆地某淤泥层为例[J]. 水文地质工程地质,2021,48(2):1 − 7. [SHI Honglei,HAO Qichen,SHAO Jingli,et al. Research on hydrogeological parameter inversion of an aquitard based on multi-source data:A case study of a silt layer in the Hohhot Basin[J]. Hydrogeology & Engineering Geology,2021,48(2):1 − 7. (in Chinese with English abstract)
SHI Honglei, HAO Qichen, SHAO Jingli, et al . Research on hydrogeological parameter inversion of an aquitard based on multi-source data: A case study of a silt layer in the Hohhot Basin[J]. Hydrogeology & Engineering Geology,2021 ,48 （2 ）:1 −7 . （in Chinese with English abstract）[24] BEAR J. Hydraulics of groundwater[M]. New York:McGraw-Hill Book Co,1979.
[25] LUO Xiaodong,STORDAL A S,LORENTZEN R J,et al. Iterative ensemble smoother as an approximate solution to a regularized minimum-average-cost problem:Theory and applications[J]. SPE Journal,2015,20(5):962 − 982. doi: 10.2118/176023-PA
[26] ZHANG Hongqin,TIAN Xiangjun. An efficient local correlation matrix decomposition approach for the localization implementation of ensemble-based assimilation methods[J]. Journal of Geophysical Research:Atmospheres,2018,123(7):3556 − 3573.
[27] ANDERSON T W. An introduction to multivariate statistical analysis[M]. 3rd ed. Hoboken:Wiley-Interscience,2003.
期刊类型引用(2)
1. 焦婷婷，邓亚平，钱家忠，骆乾坤. 基于集合平滑数据同化与直接采样法融合水文地球物理数据刻画裂隙网络分布. 水文地质工程地质. 2024(04): 88-100 . 
本站查看
2. 夏传安，樊秀峰，王浩，简文彬. 耦合变密度地下水流降阶模型与高斯过程的蒙特卡罗模拟. 水文地质工程地质. 2024(05): 1-13 . 本站查看
其他类型引用(0)
-
图(5)
表(4)
计量
- 文章访问数: 867
- PDF下载数: 85
- 施引文献: 2